A closer look at orbit integration¶
Orbit initialization¶
Standard initialization¶
Orbits can be initialized in various
coordinate frames. The simplest initialization gives the initial
conditions directly in the Galactocentric cylindrical coordinate frame
(or in the rectangular coordinate frame in one dimension). Orbit()
automatically figures out the dimensionality of the space from the
initial conditions in this case. In three dimensions initial
conditions are given either as [R,vR,vT,z,vz,phi] or one can
choose not to specify the azimuth of the orbit and initialize with
[R,vR,vT,z,vz]. Since potentials in galpy are easily initialized
to have a circular velocity of one at a radius equal to one, initial
coordinates are best given as a fraction of the radius at which one
specifies the circular velocity, and initial velocities are best
expressed as fractions of this circular velocity. For example,
>>> from galpy.orbit import Orbit
>>> o= Orbit([1.,0.1,1.1,0.,0.1,0.])
initializes a fully three-dimensional orbit, while
>>> o= Orbit([1.,0.1,1.1,0.,0.1])
initializes an orbit in which the azimuth is not tracked, as might be useful for axisymmetric potentials.
In two dimensions, we can similarly specify fully two-dimensional
orbits o=Orbit([R,vR,vT,phi]) or choose not to track the azimuth
and initialize with o= Orbit([R,vR,vT]).
In one dimension we simply initialize with o= Orbit([x,vx]).
Initialization with physical units¶
Orbits are normally used in galpy’s natural coordinates. When Orbits
are initialized using a distance scale ro= and a velocity scale
vo=, then many Orbit methods return quantities in physical
coordinates. Specifically, physical distance and velocity scales are
specified as
>>> op= Orbit([1.,0.1,1.1,0.,0.1,0.],ro=8.,vo=220.)
All output quantities will then be automatically be specified in physical units: kpc for positions, km/s for velocities, (km/s)^2 for energies and the Jacobi integral, km/s kpc for the angular momentum o.L() and actions, 1/Gyr for frequencies, and Gyr for times and periods. See below for examples of this.
The actual initial condition can also be specified in physical units. For example, the Orbit above can be initialized as
>>> from astropy import units
>>> op= Orbit([8.*units.kpc,22.*units.km/units.s,242*units.km/units.s,0.*units.kpc,22.*units.km/units.s,0.*units.deg])
In this case, it is unnecessary to specify the ro= and vo=
scales; when they are not specified, ro and vo are set to the
default values from the configuration file. However, if they are specified, then those values
rather than the ones from the configuration file are used.
Tip
If you do input and output in physical units, the internal unit conversion specified by ro= and vo= does not matter!
Inputs to any Orbit method can also be specified with units as an astropy Quantity. galpy’s natural units are still used under the hood, as explained in the section on physical units in galpy. For example, integration times can be specified in Gyr if you want to integrate for a specific time period.
If for any output you do not want the output in physical units, you
can specify this by supplying the keyword argument
use_physical=False.
Initialization from observed coordinates or astropy SkyCoord¶
For orbit integration and characterization of observed stars or
clusters, initial conditions can also be specified directly as
observed quantities when radec=True is set (see further down in
this section on how to use an astropy SkyCoord
instead). In this case a full three-dimensional orbit is initialized
as o= Orbit([RA,Dec,distance,pmRA,pmDec,Vlos],radec=True)
where RA and Dec are expressed in degrees, the distance is expressed
in kpc, proper motions are expressed in mas/yr (pmra = pmra’ *
cos[Dec] ), and Vlos is the heliocentric line-of-sight velocity
given in km/s. The observed epoch is currently assumed to be
J2000.00. These observed coordinates are translated to the
Galactocentric cylindrical coordinate frame by assuming a Solar motion
that can be specified as either solarmotion='hogg' (2005ApJ…629..268H),
solarmotion='dehnen' (1998MNRAS.298..387D) or
solarmotion='schoenrich' (default; 2010MNRAS.403.1829S). A circular
velocity can be specified as vo=220 in km/s and a value for the
distance between the Galactic center and the Sun can be given as
ro=8.0 in kpc (e.g., 2012ApJ…759..131B). While the
inputs are given in physical units, the orbit is initialized assuming
a circular velocity of one at the distance of the Sun (that is, the
orbit’s position and velocity is scaled to galpy’s natural units
after converting to the Galactocentric coordinate frame, using the
specified ro= and vo=). The parameters of the coordinate
transformations are stored internally, such that they are
automatically used for relevant outputs (for example, when the RA of
an orbit is requested). An example of all of this is:
>>> o= Orbit([20.,30.,2.,-10.,20.,50.],radec=True,ro=8.,vo=220.)
However, the internally stored position/velocity vector is
>>> print(o.vxvv)
# [1.1480792664061401, 0.1994859759019009, 1.8306295160508093, -0.13064400474040533, 0.58167185623715167, 0.14066246212987227]
and is therefore in natural units.
Tip
Initialization using observed coordinates can also use units. So, for example, proper motions can be specified as 2*units.mas/units.yr.
Similarly, one can also initialize orbits from Galactic coordinates
using o= Orbit([glon,glat,distance,pmll,pmbb,Vlos],lb=True), where
glon and glat are Galactic longitude and latitude expressed in
degrees, and the proper motions are again given in mas/yr ((pmll =
pmll’ * cos[glat] ):
>>> o= Orbit([20.,30.,2.,-10.,20.,50.],lb=True,ro=8.,vo=220.)
>>> print(o.vxvv)
# [0.79959714332811838, 0.073287283885367677, 0.5286278286083651, 0.12748861331872263, 0.89074407199364924, 0.0927414387396788]
When radec=True or lb=True is set, velocities can also be
specified in Galactic coordinates if UVW=True is set. The input is
then [RA,Dec,distance,U,V,W], where the velocities are expressed
in km/s. U is, as usual, defined as -vR (minus vR).
Finally, orbits can also be initialized using an
astropy.coordinates.SkyCoord object. For example, the (ra,dec)
example from above can also be initialized as:
>>> from astropy.coordinates import SkyCoord
>>> import astropy.units as u
>>> c= SkyCoord(ra=20.*u.deg,dec=30.*u.deg,distance=2.*u.kpc,
pm_ra_cosdec=-10.*u.mas/u.yr,pm_dec=20.*u.mas/u.yr,
radial_velocity=50.*u.km/u.s)
>>> o= Orbit(c)
In this case, you can still specify the properties of the
transformation to Galactocentric coordinates using the standard
ro, vo, zo, and solarmotion keywords, or you can use
the SkyCoord Galactocentric frame specification
and these are propagated to the Orbit instance. For example,
>>> from astropy.coordinates import CartesianDifferential
>>> c= SkyCoord(ra=20.*u.deg,dec=30.*u.deg,distance=2.*u.kpc,
pm_ra_cosdec=-10.*u.mas/u.yr,pm_dec=20.*u.mas/u.yr,
radial_velocity=50.*u.km/u.s,
galcen_distance=8.*u.kpc,z_sun=15.*u.pc,
galcen_v_sun=CartesianDifferential([10.0,235.,7.]*u.km/u.s))
>>> o= Orbit(c)
A subtlety here is that the galcen_distance and ro keywords
are not interchangeable, because the former is the distance between
the Sun and the Galactic center and ro is the projection of this
distance onto the Galactic midplane. Another subtlety is that the
astropy Galactocentric frame is a right-handed frame, while galpy
normally uses a left-handed frame, so the sign of the x component of
galcen_v_sun is the opposite of what it would be in
solarmotion. Because the Galactocentric frame in astropy does
not specify the circular velocity, but only the Sun’s velocity, you
still need to specify vo to use a non-default circular velocity.
When orbits are initialized using radec=True, lb=True, or
using a SkyCoord physical scales ro= and vo= are
automatically specified (because they have defaults of ro=8 and
vo=220). Therefore, all output quantities will be specified in
physical units (see above). If you do want to get outputs in galpy’s
natural coordinates, you can turn this behavior off by doing
>>> o.turn_physical_off()
All outputs will then be specified in galpy’s natural coordinates.
Initializing multiple objects at once¶
In all of the examples above, the Orbit instance corresponds to a
single object, but Orbit instances can also contain and analyze
multiple objects at once. This makes handling Orbit instances
highly convenient and also allows for efficient handling of multiple
objects. Many of the most computationally-intense methods have been
parallelized (orbit integration; analytic eccentricity, zmax,
etc. calculation; action-angle calculations) and some other methods
switch to more efficient algorithms for larger numbers of objects
(e.g., rguiding, rE, LcE).
All of the methods for initializing Orbit instances above work for
multiple objects. Specifically, the initial conditions can be:
- Array of arbitrary shape (shape,phasedim); needs to be in internal units (for Quantity input; see ‘list’ option below or use a SkyCoord):
in Galactocentric cylindrical coordinates with phase-space coordinates arranged as [R,vR,vT(,z,vz,phi)];
[ra,dec,d,mu_ra, mu_dec,vlos] or [l,b,d,mu_l, mu_b, vlos] in [deg,deg,kpc,mas/yr,mas/yr,km/s], or [ra,dec,d,U,V,W] or [l,b,d,U,V,W] in [deg,deg,kpc,km/s,km/s,kms] (ICRS where relevant; mu_ra = mu_ra * cos dec and mu_l = mu_l * cos ); use the
radec=,lb=, andUVW=keywords as before
astropy (>v3.0) SkyCoord with arbitrary shape, including velocities;
- lists of initial conditions, entries can be
individual Orbit instances (of single objects)
Regular or Quantity arrays arranged as in the first bullet above (so things like [R,vR,vT,z,vz,phi], where R, vR, … can be arbitrary shape regular or Quantity arrays)
list of Quantities (so things like [R1,vR1,..,], where R1, vR1, … are scalar Quantities
None: assumed to be the Sun; if None occurs in a list it is assumed to be the Sun and all other items in the list are assumed to be [ra,dec,…]; cannot be combined with Quantity lists
lists of scalar phase-space coordinates arranged as in the first bullet above (so things like [R,vR,…] where R,vR are scalars in internal units
The solar parameters ro, zo, vo, and solarmotion can also be specified as arrays with the same shape as the resulting Orbit instance. This can be useful, for example, when sampling over the uncertainty in the Sun’s position and velocity in the Milky Way.
Tip
For multiple object initialization using an array or SkyCoord, arbitrary input shapes are supported.
An example initialization with an array is:
>>> vxvvs= numpy.array([[1.,0.1,1.,0.1,-0.2,1.5],[0.1,0.3,1.1,-0.3,0.4,2.]])
>>> orbits= Orbit(vxvvs)
>>> print(orbits.R())
# [ 1. 0.1]
and with a SkyCoord:
>>> numpy.random.seed(1)
>>> nrand= 30
>>> ras= numpy.random.uniform(size=nrand)*360.*u.deg
>>> decs= 90.*(2.*numpy.random.uniform(size=nrand)-1.)*u.deg
>>> dists= numpy.random.uniform(size=nrand)*10.*u.kpc
>>> pmras= 20.*(2.*numpy.random.uniform(size=nrand)-1.)*20.*u.mas/u.yr
>>> pmdecs= 20.*(2.*numpy.random.uniform(size=nrand)-1.)*20.*u.mas/u.yr
>>> vloss= 200.*(2.*numpy.random.uniform(size=nrand)-1.)*u.km/u.s
# Without any custom coordinate-transformation parameters
>>> co= SkyCoord(ra=ras,dec=decs,distance=dists,
pm_ra_cosdec=pmras,pm_dec=pmdecs,
radial_velocity=vloss,
frame='icrs')
>>> orbits= Orbit(co)
>>> print(orbits.ra()[:3],ras[:3])
# [ 1.50127922e+02 2.59316818e+02 4.11749371e-02] deg [ 1.50127922e+02 2.59316818e+02 4.11749342e-02] deg
As before, you can use the SkyCoord Galactocentric frame
specification here.
An example initialization with array input for ro is:
>>> vxvvs= numpy.array([[1.,0.1,1.,0.1,-0.2,1.5] for ii in range(2)])
>>> orbits= Orbit(vxvvs,ro=numpy.array([8.,8.5]))
>>> print(orbits.R())
# [ 8. 8.5]
Array inputs can also be used for zo, vo, and solarmotion. When using arrays,
their shapes need to agree with the shape of the resulting Orbit instance (for
solarmotion, the shape needs to be [3,*shape_orbit]).
Orbit instances containing multiple objects act like numpy arrays
in many ways, but have some subtly different behaviors for some
functions. For example, one can do:
>>> print(len(orbits))
# 30
>>> print(orbits.shape)
# (30,)
>>> print(orbits.size)
# 30
>>> orbits.reshape((6,5)) # reshape is done inplace
>>> print(len(orbits))
# 6
>>> print(orbits.shape)
# (6,5)
>>> print(orbits.size)
# 30
>>> sliced_orbits= orbits[:3,1:5] # Extract a subset using numpy's slicing rules
>>> print(sliced_orbits.shape)
# (3,4)
>>> single_orbit= orbits[1,3] # Extract a single object
>>> print(single_orbit.shape)
# ()
Slicing creates a new Orbit instance. When slicing an Orbit
instance that has been integrated, the integrated orbit will be
transferred to the new instance.
The shape of the Orbit instances is retained for all relevant
outputs. Continuing on from the previous example (where orbits has
shape (6,5) after we reshaped it), we have:
>>> print(orbits.R().shape)
# (6,5)
>>> print(orbits.L().shape)
# (6,5,3)
After orbit integration, evaluating orbits.R(times) would return
an array with shape (6,5,ntimes) here.
Initialization from an object’s name¶
A convenience method, Orbit.from_name, is also available to initialize
orbits from the name of an object. For example, for the star Lacaille 8760:
>>> o= Orbit.from_name('Lacaille 8760', ro=8., vo=220.)
>>> [o.ra(), o.dec(), o.dist(), o.pmra(), o.pmdec(), o.vlos()]
# [319.31362023999276, -38.86736390000036, 0.003970940656277758, -3258.5529999996584, -1145.3959999996205, 20.560000000006063]
but this also works for globular clusters, e.g., to obtain Omega Cen’s orbit and current location in the Milky Way do:
>>> o= Orbit.from_name('Omega Cen')
>>> from galpy.potential import MWPotential2014
>>> ts= numpy.linspace(0.,100.,2001)
>>> o.integrate(ts,MWPotential2014)
>>> o.plot()
>>> plot([o.R()],[o.z()],'ro')
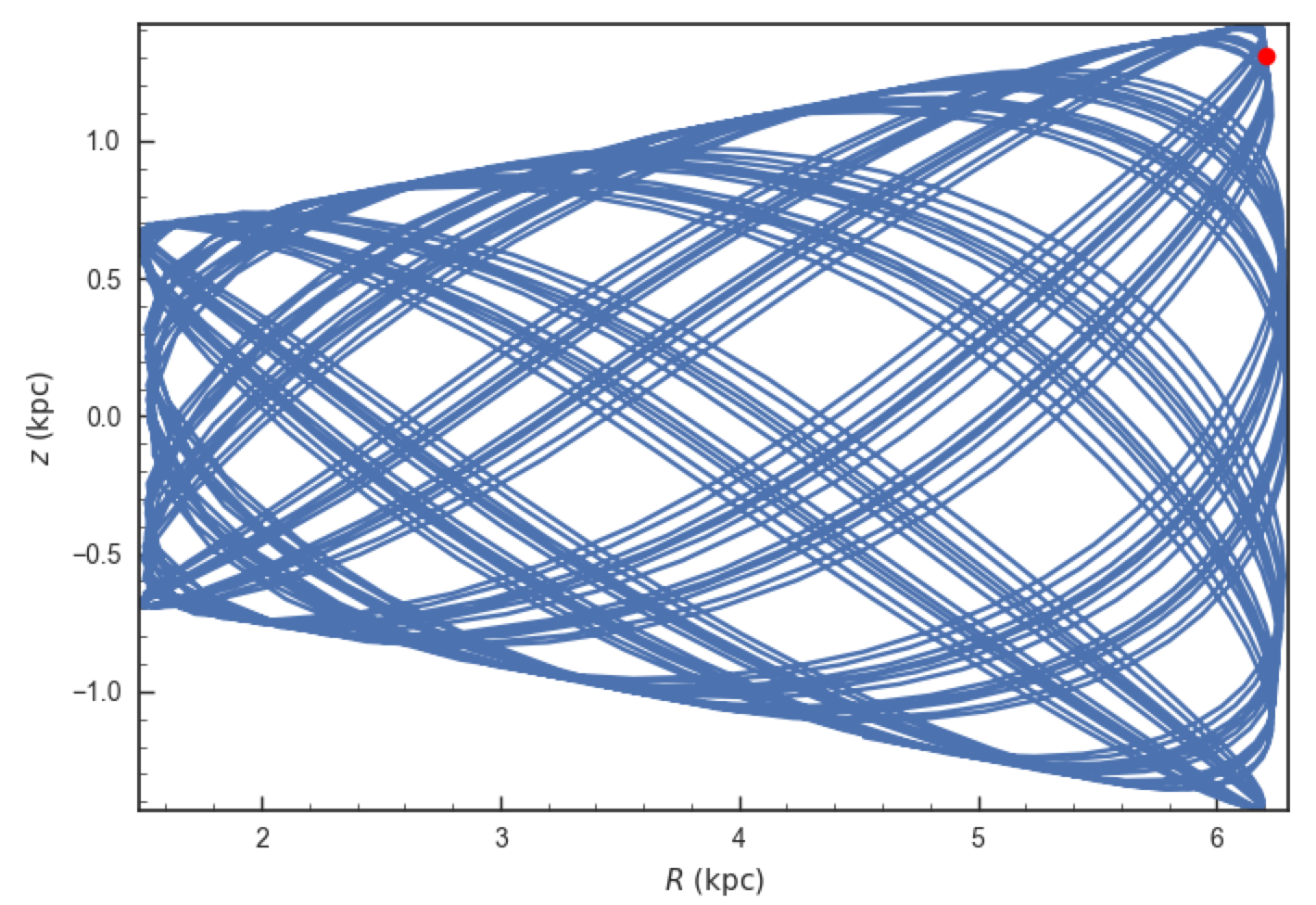
We see that Omega Cen is currently close to its maximum distance from both the Galactic center and from the Galactic midplane (note that Omega Cen’s phase-space coordinates were updated internally in galpy after this plot was made and the orbit is now slightly different).
Similarly, you can do:
>>> o= Orbit.from_name('LMC')
>>> [o.ra(), o.dec(), o.dist(), o.pmra(), o.pmdec(), o.vlos()]
# [80.894200000000055, -69.756099999999847, 49.999999999999993, 1.909999999999999, 0.2290000000000037, 262.19999999999993]
It is also possible to initialize using multiple names, for example:
>>> o= Orbit.from_name(['LMC','SMC'])
>>> print(o.ra(),o.dec(),o.dist())
# [ 80.8942 13.1583] deg [-69.7561 -72.8003] deg [ 50. 60.] kpc
The names are stored in the name attribute:
>>> print(o.name)
# ['LMC', 'SMC']
The Orbit.from_name method attempts to resolve the name of the
object in SIMBAD, and then use the observed coordinates found there to
generate an Orbit instance. In order to query SIMBAD,
Orbit.from_name requires the astroquery package to be installed. A
small number of objects, mainly Milky Way globular clusters and dwarf
satellite galaxies, have their phase-space coordinates stored in a
file that is part of galpy and for these objects the values from this
file are used rather than querying SIMBAD. Orbit.from_name
supports tab completion in IPython/Jupyter for this list of objects

The Orbit.from_name method also allows you to load some
collections of objects in a simple manner. Currently, three
collections are supported: ‘MW globular clusters’, ‘MW satellite
galaxies’, and ‘solar system’. Specifying ‘MW globular clusters’ loads
all of the Milky-Way globular clusters with data from Gaia EDR3:
>>> o= Orbit.from_name('MW globular clusters')
>>> print(len(o))
# 161
>>> print(o.name)
# ['NGC5286' 'Terzan12' 'Arp2', ... ]
>>> print(o.r())
# [ 8.4418065 2.99042499 21.55042257 ...]
It is then easy to, for example, integrate the orbits of all Milky-Way globular clusters in MWPotential2014 and plot them in 3D:
>>> ts= numpy.linspace(0.,300.,1001)
>>> o.integrate(ts,MWPotential2014)
>>> o.plot3d(alpha=0.4)
>>> xlim(-100.,100.)
>>> ylim(-100.,100)
>>> gca().set_zlim3d(-100.,100);
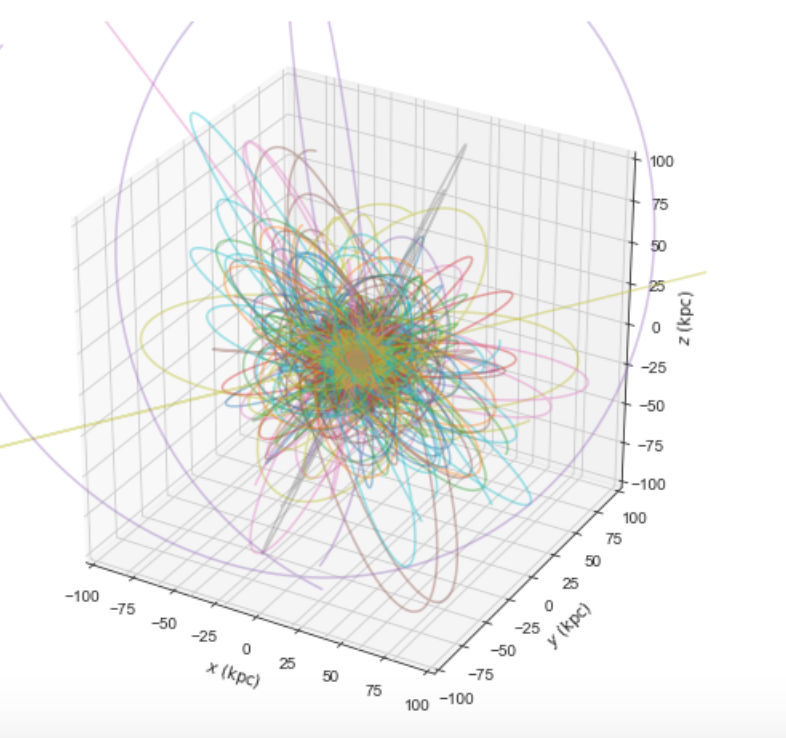
Similarly, ‘MW satellite galaxies’ loads all of the Milky-Way satellite galaxies from Pace et al. (2022):
>>> o= Orbit.from_name('MW satellite galaxies')
>>> print(len(o))
# 50
>>> print(o.name)
# ['AntliaII' 'AquariusII' 'BootesI' 'BootesII' 'BootesIII' 'CanesVenaticiI'
'CanesVenaticiII' 'Carina' 'CarinaII' 'CarinaIII' 'ColumbaI'
'ComaBerenices' 'CraterII' 'Draco' 'DracoII' 'EridanusII' 'Fornax'
'GrusI' 'GrusII' 'Hercules' 'HorologiumI' 'HydraII' 'HydrusI' 'LMC'
'LeoI' 'LeoII' 'LeoIV' 'LeoV' 'PegasusIII' 'PhoenixI' 'PhoenixII'
'PiscesII' 'ReticulumII' 'ReticulumIII' 'SMC' 'SagittariusII' 'Sculptor'
'Segue1' 'Segue2' 'Sextans' 'Sgr' 'TriangulumII' 'TucanaII' 'TucanaIII'
'TucanaIV' 'TucanaV' 'UrsaMajorI' 'UrsaMajorII' 'UrsaMinor' 'Willman1']
>>> print(o.r())
# [132.93721433 105.41442453 63.66115037 39.83901891 45.52928256
209.7700823 160.60534628 107.16399152 38.24845108 28.9274277
187.46809402 43.16546984 116.44003784 75.80593376 23.71949352
367.79884477 149.18728196 123.27421442 50.52704455 125.11664692
79.292941 148.20468685 25.74545627 49.60813235 261.93577755
235.49080095 151.95997497 169.77910104 213.08771512 418.76813979
81.18196715 182.15380106 32.72475876 91.96956471 60.28760354
63.35088903 83.99141137 27.77404178 42.42833236 95.44075955
19.06561359 34.54212398 54.28214129 21.05199179 44.4906331
51.92586773 101.87656784 40.73034335 78.06428801 42.6385771 ] kpc
and we can integrate and plot them in 3D as above:
>>> o.plot3d(alpha=0.4)
>>> xlim(-400.,400.)
>>> ylim(-400.,400)
>>> gca().set_zlim3d(-400.,400)
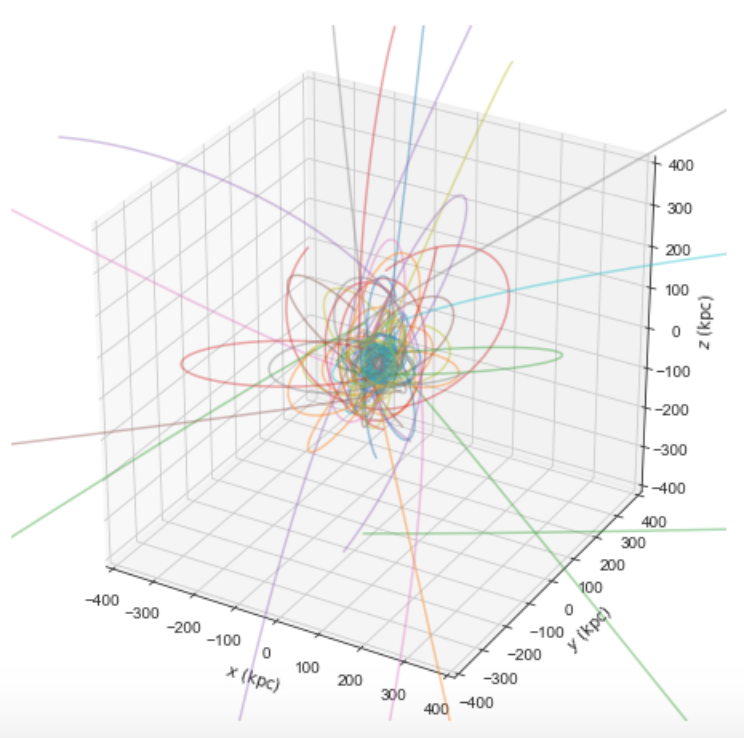
Because MWPotential2014 has a relatively low-mass dark-matter halo, a bunch of the satellites are unbound (to make them bound, you can increase the mass of the halo by, for example, multiplying it by 1.5, as in MWPotential2014[2]*= 1.5).
Finally, for illustrative purposes, the solar system is included as a
collection as well. The solar system is set up such that the center of
what is normally the Galactocentric coordinate frame in galpy is
now the solar system barycenter and the coordinate frame is a
heliocentric one. The solar system data are taken from Bovy et
al. (2010)
and they represent the positions and planets on April 1, 2009. To load
the solar system do:
>>> o= Orbit.from_name('solar system')
Giving for example:
>>> print(o.name)
# ['Mercury', 'Venus', 'Earth', 'Mars', 'Jupiter', 'Saturn', 'Uranus', 'Neptune']
You can then, for example, integrate the solar system for 10 years as follows
>>> import astropy.units as u
>>> from galpy.potential import KeplerPotential
>>> from galpy.util.conversion import get_physical
>>> kp= KeplerPotential(amp=1.*u.Msun,**get_physical(o)) # Need to use **get_physical to get the ro= and vo= parameters, which differ from the default for the solar system
>>> ts= numpy.linspace(0.,10.,1001)*u.yr
>>> o.integrate(ts,kp)
>>> o.plot(d1='x',d2='y')
which gives
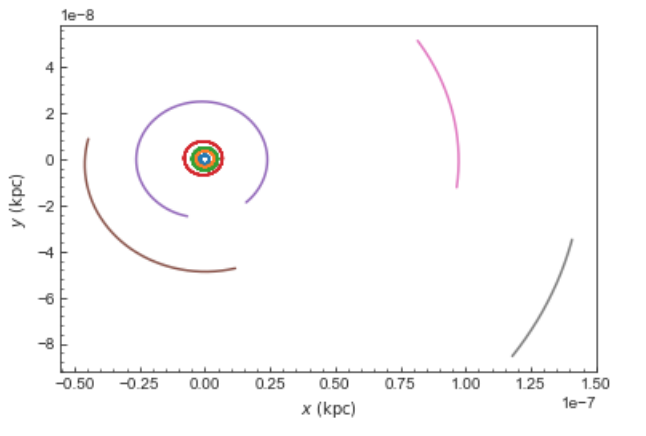
Note that, as usual, physical outputs are in kpc, leading to very small numbers!
Tip
Setting up an Orbit instance without arguments will return an Orbit instance representing the Sun: o= Orbit(). This instance has physical units turned on by default, so methods will return outputs in physical units unless you o.turn_physical_off().
Warning
Orbits initialized using Orbit.from_name have physical output turned on by default, so methods will return outputs in physical units unless you o.turn_physical_off().
Orbit integration¶
After an orbit is initialized, we can integrate it for a set of times
ts, given as a numpy array. For example, in a simple logarithmic
potential we can do the following
>>> from galpy.potential import LogarithmicHaloPotential
>>> lp= LogarithmicHaloPotential(normalize=1.)
>>> o= Orbit([1.,0.1,1.1,0.,0.1,0.])
>>> import numpy
>>> ts= numpy.linspace(0,100,10000)
>>> o.integrate(ts,lp)
to integrate the orbit from t=0 to t=100, saving the orbit at
10000 instances. In physical units, we can integrate for 10 Gyr as follows
>>> from astropy import units
>>> ts= numpy.linspace(0,10.,10000)*units.Gyr
>>> o.integrate(ts,lp)
Warning
When the integration times are not specified using a Quantity, they are assumed to be in natural units.
If we initialize the Orbit using a distance scale ro= and a
velocity scale vo=, then Orbit plots and outputs will use physical
coordinates (currently, times, positions, and velocities)
>>> op= Orbit([1.,0.1,1.1,0.,0.1,0.],ro=8.,vo=220.) #Use Vc=220 km/s at R= 8 kpc as the normalization
>>> op.integrate(ts,lp)
An Orbit instance containing multiple objects can be integrated in
the same way and the orbit integration will be performed in parallel
on machines with multiple cores. For the fast C integrators (see
below), this parallelization is done using OpenMP in C
and requires one to set the OMP_NUM_THREADS environment variable
to control the number of cores used. The Python integrators are
parallelized in Python and by default also use the OMP_NUM_THREADS
variable to set the number of cores (but for the Python integrators
this can be overwritten). A simple example is
>>> vxvvs= numpy.array([[1.,0.1,1.,0.1,-0.2,1.5],[0.1,0.3,1.1,-0.3,0.4,2.]])
>>> orbits= Orbit(vxvvs)
>>> orbits.integrate(ts,lp)
>>> print(orbits.R(ts).shape)
# (2,10000)
>>> print(orbits.R(ts))
# [[ 1. 1.00281576 1.00563403 ..., 1.05694767 1.05608923
# 1.0551804 ]
# [ 0.1 0.18647825 0.27361065 ..., 3.39447863 3.34992543
# 3.30527001]]
Orbit integration in non-inertial frames¶
The default assumption in galpy is that the frame that an orbit is
integrated in is an inertial one. However, galpy also supports
orbit integration in non-inertial frames that are rotating or whose
center is accelerating (or a combination of the two). When a frame is
not an inertial frame, fictitious forces such as the centrifugal
and Coriolis forces need to be taken into account. galpy implements
all of the necessary forces as part of the
NonInertialFrameForce class. objects
of this class are instantiated with arbitrary three-dimensional rotation
frequencies (and their time derivative) and/or arbitrary three-dimensional
acceleration of the origin. The class documentation linked to above
provides full mathematical details on the rotation and acceleration
of the non-inertial frame.
We can then, for example, integrate the orbit of the Sun in the LSR frame,
that is, the frame that is corotating with that of the circular orbit
at the location of the Sun. To do this for MWPotential2014, do
>>> from galpy.potential import MWPotential2014, NonInertialFrameForce
>>> nip= NonInertialFrameForce(Omega=1.) # LSR has Omega=1 in natural units
>>> o= Orbit() # Orbit() is the orbit of the Sun in the inertial frame
>>> o.turn_physical_off() # To use internal units
>>> o= Orbit([o.R(),o.vR(),o.vT()-1.,o.z(),o.vz(),o.phi()]) # Convert to the LSR frame
>>> ts= numpy.linspace(0.,20.,1001)
>>> o.integrate(ts,MWPotential2014+nip)
>>> o.plot(d1='x',d2='y')
which gives
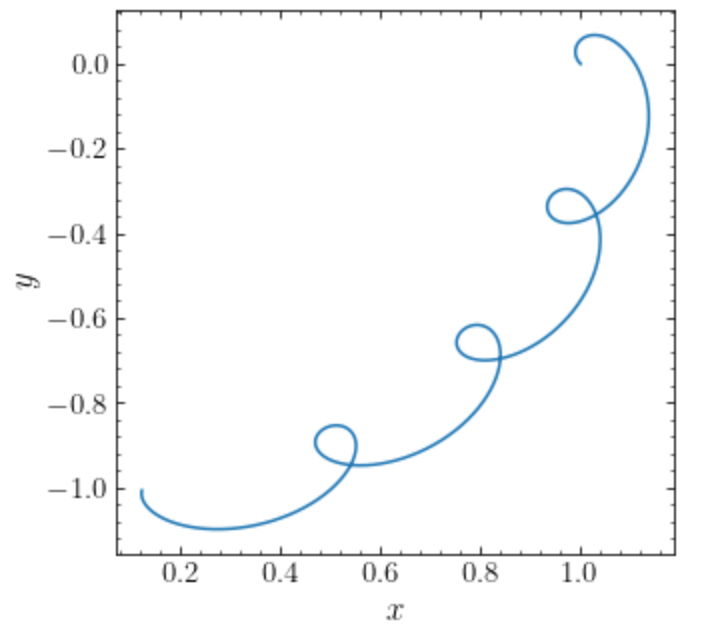
we can compare this to integrating the orbit in the inertial frame and displaying it in the non-inertial LSR frame as follows:
>>> o.plot(d1='x',d2='y') # Repeat plot from above
>>> o= Orbit() # Orbit() is the orbit of the Sun in the inertial frame
>>> o.turn_physical_off() # To use internal units
>>> o.integrate(ts,MWPotential2014)
>>> o.plot(d1='R*cos(phi-t)',d2='R*sin(phi-t)',overplot=True) # Omega = 1, so Omega t = t
which gives
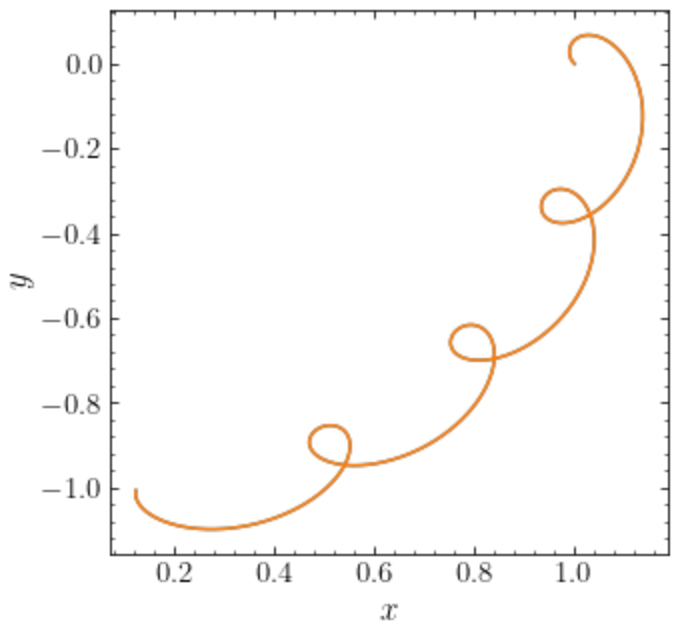
We can also do all of the above in physical units, in which case the first example above becomes
>>> from galpy.potential import MWPotential2014, NonInertialFrameForce
>>> from astropy import units
>>> nip= NonInertialFrameForce(Omega=220./8.*units.km/units.s/units.kpc)
>>> o= Orbit() # Orbit() is the orbit of the Sun in the inertial frame
>>> o= Orbit([o.R(quantity=True),o.vR(quantity=True),
o.vT(quantity=True)-220.*units.km/units.s,
o.z(quantity=True),o.vz(quantity=True),
o.phi(quantity=True)]) # Convert to the LSR frame
>>> ts= numpy.linspace(0.,20.,1001)
>>> o.integrate(ts,MWPotential2014+nip)
>>> o.plot(d1='x',d2='y')
We can also provide the Omega= frequency as an arbitrary function of time.
In this case, the frequency must be returned in internal units and the input
time of this function must be in internal units as well (use the routines in
galpy.util.conversion for converting from physical to
internal units; you need to divide by these to go from physical to internal).
For the example above, this would amount to setting
>>> nip= NonInertialFrameForce(Omega=lambda t: 1.,Omegadot=lambda t: 0.)
Note that when we supply Omega as a function, it is necessary to specify
its time derivative as well as Omegadot (all again in internal units).
We give an example of having the origin of the non-inertial frame accelerate in the Example: Including the Milky Way center’s barycentric acceleration due to the Large Magellanic Cloud in orbit integrations section below.
Displaying the orbit¶
After integrating the orbit, it can be displayed by using the
plot() function. The quantities that are plotted when plot()
is called depend on the dimensionality of the orbit: in 3D the (R,z)
projection of the orbit is shown; in 2D either (X,Y) is plotted if the
azimuth is tracked and (R,vR) is shown otherwise; in 1D (x,vx) is
shown. E.g., for the example given above at the start of the
Orbit integration section above,
>>> o.plot()
gives
If we do the same for the Orbit that has physical distance and velocity scales associated with it, we get the following
>>> op.plot()
If we call op.plot(use_physical=False), the quantities will be
displayed in natural galpy coordinates.
Plotting an Orbit instance that consists of multiple objects plots
all objects at once, e.g.,
>>> orbits.plot()
gives
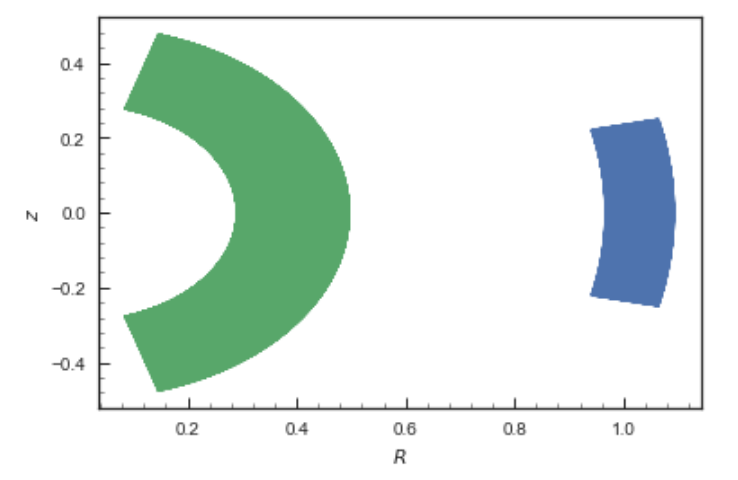
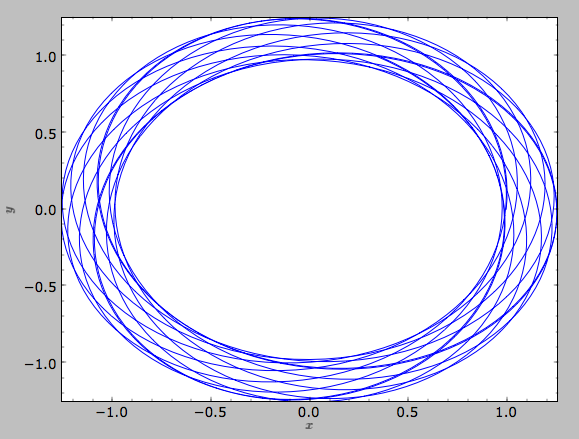
Other projections of the orbit can be displayed by specifying the quantities to plot. E.g.,
>>> o.plot(d1='x',d2='y')
gives the projection onto the plane of the orbit:
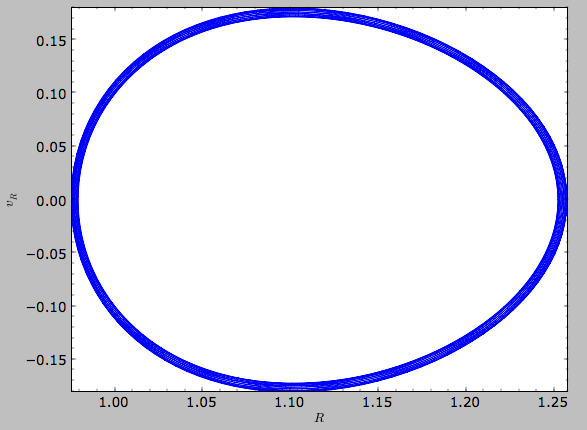
while
>>> o.plot(d1='R',d2='vR')
gives the projection onto (R,vR):
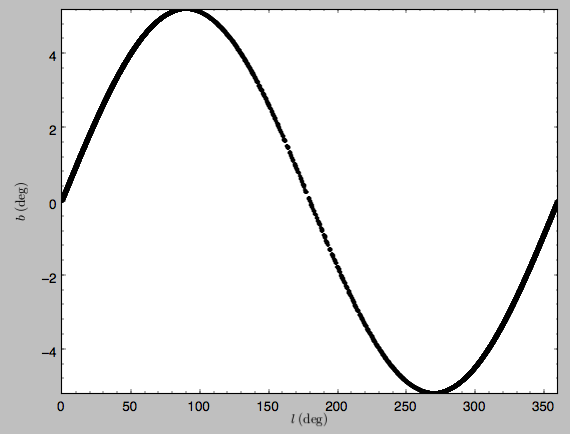
We can also plot the orbit in other coordinate systems such as Galactic longitude and latitude
>>> o.plot('k.',d1='ll',d2='bb')
which shows
or RA and Dec
>>> o.plot('k.',d1='ra',d2='dec')
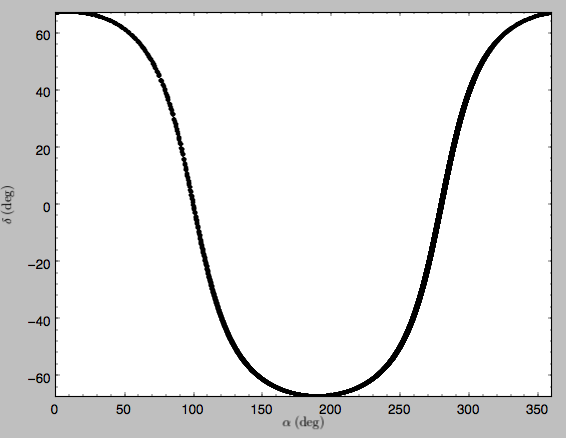
See the documentation of the o.plot function and the o.ra(), o.ll(), etc. functions on how to provide the necessary parameters for the coordinate transformations.
It is also possible to plot quantities computed from the basic Orbit
outputs like o.x(), o.r(), etc. For this to work, the numexpr module needs to be installed;
this can be done using pip or conda. Then you can ask for
plots like
>>> o.plot(d1='r',d2='vR*R/r+vz*z/r')
where d2= converts the velocity to spherical coordinates (this is
currently not a pre-defined option). This gives the following orbit
(which is closed in this projection, because we are using a spherical
potential):
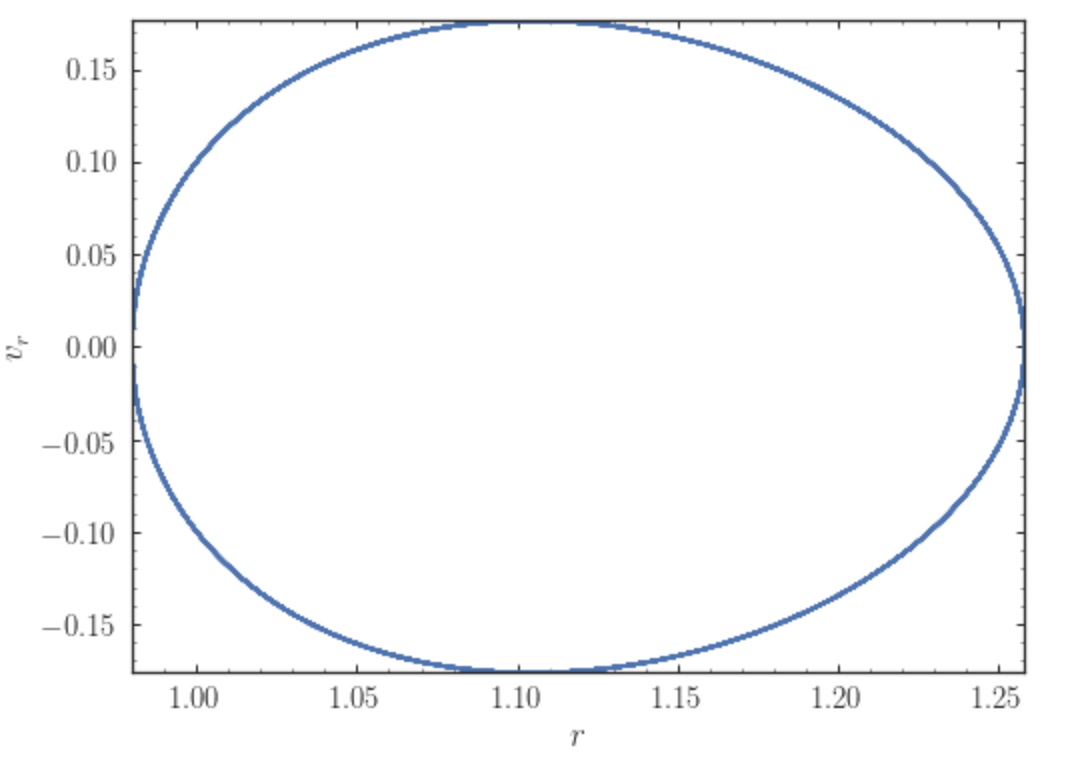
You can also do more complex things like
>>> o.plot(d1='x',d2='y')
>>> o.plot(d1='R*cos(phi-{:f}*t)'.format(o.Op(quantity=False)),
d2='R*sin(phi-{:f}*t)'.format(o.Op(quantity=False)),
overplot=True)
which shows the orbit in the regular (x,y) frame as well as in a
(x,y) frame that is rotating at the angular frequency of the
orbit. When doing more complex calculations like this, you need to
make sure that you are getting the units right: parameters param
in the expression you provide are directly evaluated as o.param(),
which depending on how you setup the object may or may not return
output in physical units. The expression above is safe, because
o.Op evaluated like this will be in a consistent unit system with
the rest of the expression. Expressions cannot contain astropy
Quantities (these cannot be parsed by the parser), which is why
quantity=False is specified; this is also used internally.
Finally, it is also possible to plot arbitrary functions of time with
Orbit.plot, by specifying d1= or d2= as a function. For
example, to display the orbital velocity in the spherical radial
direction, which we also did with the expression above, you can do the
following
>>> o.plot(d1='r',
d2=lambda t: o.vR(t)*o.R(t)/o.r(t)+o.vz(t)*o.z(t)/o.r(t),
ylabel='v_r')
For a function like this, just specifying it as the expression
d2='vR*R/r+vz*z/r' is much more convenient, but expressions that
cannot be parsed automatically could be directly given as a function.
Animating the orbit¶
Warning
Animating orbits is a new, experimental feature at this time that may be changed in later versions. It has only been tested in a limited fashion. If you are having problems with it, please open an Issue and list all relevant details about your setup (python version, jupyter version, browser, any error message in full). It may also be helpful to check the javascript console for any errors.
In a jupyter notebook or in jupyterlab (jupyterlab versions >= 0.33) you can also create an animation of an orbit after you have integrated it. For example, to do this for the op orbit from above (but only integrated for 2 Gyr to create a shorter animation as an example here), do
>>> op.animate()
This will create the following animation
Tip
There is currently no option to save the animation within galpy, but you could use screen capture software (for example, QuickTime’s Screen Recording feature) to record your screen while the animation is running and save it as a video.
animate has options to specify the width and height of the resulting animation, and it can also animate up to three projections of an orbit at the same time. For example, we can look at the orbit in both (x,y) and (R,z) at the same time with
>>> op.animate(d1=['x','R'],d2=['y','z'],width=800)
which gives
You can also animate orbit in 3D with an optional Milky Way galaxy centered at the origin
>>> op.animate3d(mw_plane_bg=True)
which gives
If you want to embed the animation in a webpage, you can obtain the necessary HTML using the _repr_html_() function of the IPython.core.display.HTML object returned by animate. By default, the HTML includes the entire orbit’s data, but animate also has an option to store the orbit in a separate JSON file that will then be loaded by the output HTML code.
animate and animate3d also work for Orbit instances containing multiple objects.
Orbit characterization¶
The properties of the orbit can also be found using galpy. For example, we can calculate the peri- and apocenter radii of an orbit, its eccentricity, and the maximal height above the plane of the orbit
>>> o.rap(), o.rperi(), o.e(), o.zmax()
# (1.2581455175173673,0.97981663263371377,0.12436710999105324,0.11388132751079502)
or for multiple objects at once
>>> orbits.rap(), orbits.rperi(), orbits.e(), orbits.zmax()
# (array([ 1.0918143 , 0.49557137]),
# array([ 0.96779816, 0.29150873]),
# array([ 0.06021334, 0.2592654 ]),
# array([ 0.24734084, 0.47327396]))
These four quantities can also be computed using analytical means (exact or approximations depending on the potential) by specifying analytic=True
>>> o.rap(analytic=True), o.rperi(analytic=True), o.e(analytic=True), o.zmax(analytic=True)
# (1.2581448917376636,0.97981640959995842,0.12436697719989584,0.11390708640305315)
or for multiple objects at once (this calculation is done in parallel on systems that support it)
>>> orbits.rap(analytic=True), orbits.rperi(analytic=True), orbits.e(analytic=True), orbits.zmax(analytic=True)
# (array([ 1.09181433, 0.49557137]),
# array([ 0.96779816, 0.29150873]),
# array([ 0.06021335, 0.2592654 ]),
# array([ 0.24734693, 0.4733304 ]))
We can also calculate the energy of the orbit, either in the potential that the orbit was integrated in, or in another potential:
>>> o.E(), o.E(pot=mp)
# (0.6150000000000001, -0.67390625000000015)
where mp is the Miyamoto-Nagai potential of Introduction:
Rotation curves.
Many other quantities characterizing the orbit can be calculated as well,
for example, orbital actions, frequencies, and angles (see
this section), the guiding-center radius rguiding,
and the radius rE and angular momentum LcE of the circular orbit
with the same energy as the Orbit instance. See the
Orbit API page for a full list of quantities that can
accessed for any Orbit instance.
For the Orbit op that was initialized above with a distance scale
ro= and a velocity scale vo=, these outputs are all in
physical units
>>> op.rap(), op.rperi(), op.e(), op.zmax()
# (10.065158988860341,7.8385312810643057,0.12436696983841462,0.91105035688072711) #kpc
>>> op.E(), op.E(pot=mp)
# (29766.000000000004, -32617.062500000007) #(km/s)^2
We can also show the energy as a function of time (to check energy conservation)
>>> o.plotE(normed=True)
gives
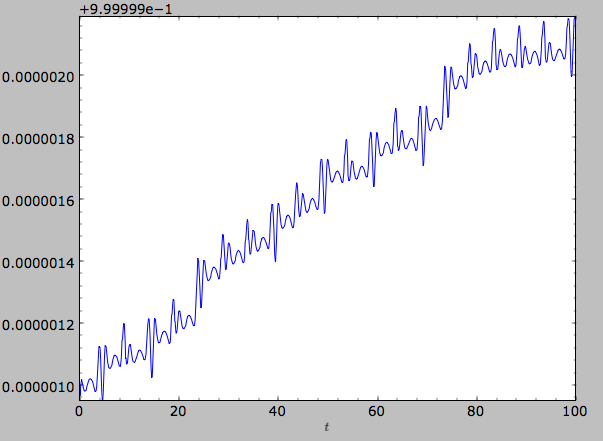
We can specify another quantity to plot the energy against by
specifying d1=. We can also show the vertical energy, for example,
as a function of R
>>> o.plotEz(d1='R',normed=True)
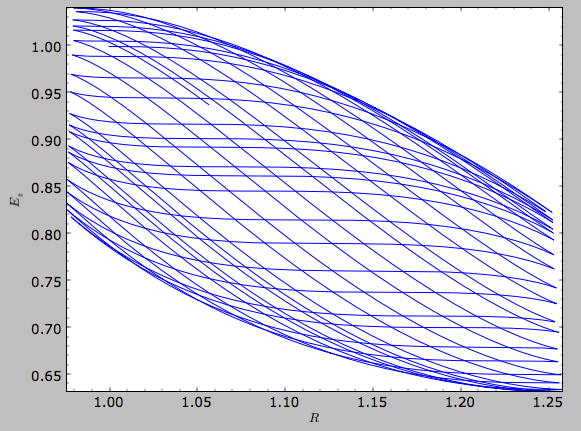
Fast orbit characterization¶
It is also possible to use galpy for the fast estimation of orbit
parameters as demonstrated in Mackereth & Bovy (2018) via the
Staeckel approximation (originally used by Binney (2012) for the
approximation of actions in axisymmetric potentials), without
performing any orbit integration. The method uses the geometry of the
orbit tori to estimate the orbit parameters. After initialising an
Orbit instance, the method is applied by specifying
analytic=True and selecting type='staeckel'.
>>> o.e(analytic=True, type='staeckel')
if running the above without integrating the orbit, the potential should also be specified in the usual way
>>> o.e(analytic=True, type='staeckel', pot=mp)
This interface automatically estimates the necessary delta parameter
based on the initial condition of the Orbit object. (delta is the
focal-length parameter of the prolate spheroidal coordinate system
used in the approximation, see the documentation of the
actionAngleStaeckel class).
While this is useful and fast for individual Orbit objects, it is
likely that users will want to rapidly evaluate the orbit parameters
of large numbers of objects. The easiest way to do this is by setting
up an Orbit instance that contains all objects and call the same
functions as above (in this case, the necessary delta parameter will
be automatically determined for each object in the instance based on
its initial condition)
>>> os= Orbit([R, vR, vT, z, vz, phi])
>>> os.e(analytic=True,type='staeckel',pot=mp)
In this case, the returned array has the same shape as the input
R,vR,... arrays.
Rather than automatically estimating delta, you can specify an array
for delta when calling os.e (or zmax, rperi, and
rap), for example by first estimating good delta parameters as
follows:
>>> from galpy.actionAngle import estimateDeltaStaeckel
>>> delta= estimateDeltaStaeckel(mp, R, z, no_median=True)
where no_median=True specifies that the function return the delta
parameter at each given point rather than the median of the calculated
deltas (which is the default option). Then one can compute the
eccentricity etc. using individual delta values as:
>>> os.e(analytic=True,type='staeckel',pot=mp,delta=delta)
We can test the speed of this method in iPython by finding the parameters at 100000 steps along an orbit in MWPotential2014, like this
>>> o= Orbit([1.,0.1,1.1,0.,0.1,0.])
>>> ts = numpy.linspace(0,100,10000)
>>> o.integrate(ts,MWPotential2014)
>>> os= o(ts) # returns an Orbit instance with nt objects, each initialized at the position at one of the ts
>>> delta= estimateDeltaStaeckel(MWPotential2014,o.R(ts),o.z(ts),no_median=True)
>>> %timeit -n 10 os.e(analytic=True,pot=MWPotential2014,delta=delta)
# 584 ms ± 8.63 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
you can see that in this potential, each phase space point is
calculated in roughly 60µs. further speed-ups can be gained by using
the galpy.actionAngle.actionAngleStaeckelGrid module, which first
calculates the parameters using a grid-based interpolation
>>> from galpy.actionAngle import actionAngleStaeckelGrid
>>> R, vR, vT, z, vz, phi = o.getOrbit().T
>>> aASG= actionAngleStaeckelGrid(pot=MWPotential2014,delta=0.4,nE=51,npsi=51,nLz=61,c=True,interpecc=True)
>>> %timeit -n 10 es, zms, rps, ras = aASG.EccZmaxRperiRap(R,vR,vT,z,vz,phi)
# 47.4 ms ± 5.11 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
where interpecc=True is required to perform the interpolation of
the orbit parameter grid. Looking at how the eccentricity estimation
varies along the orbit, and comparing to the calculation using the
orbit integration, we see that the estimation good job
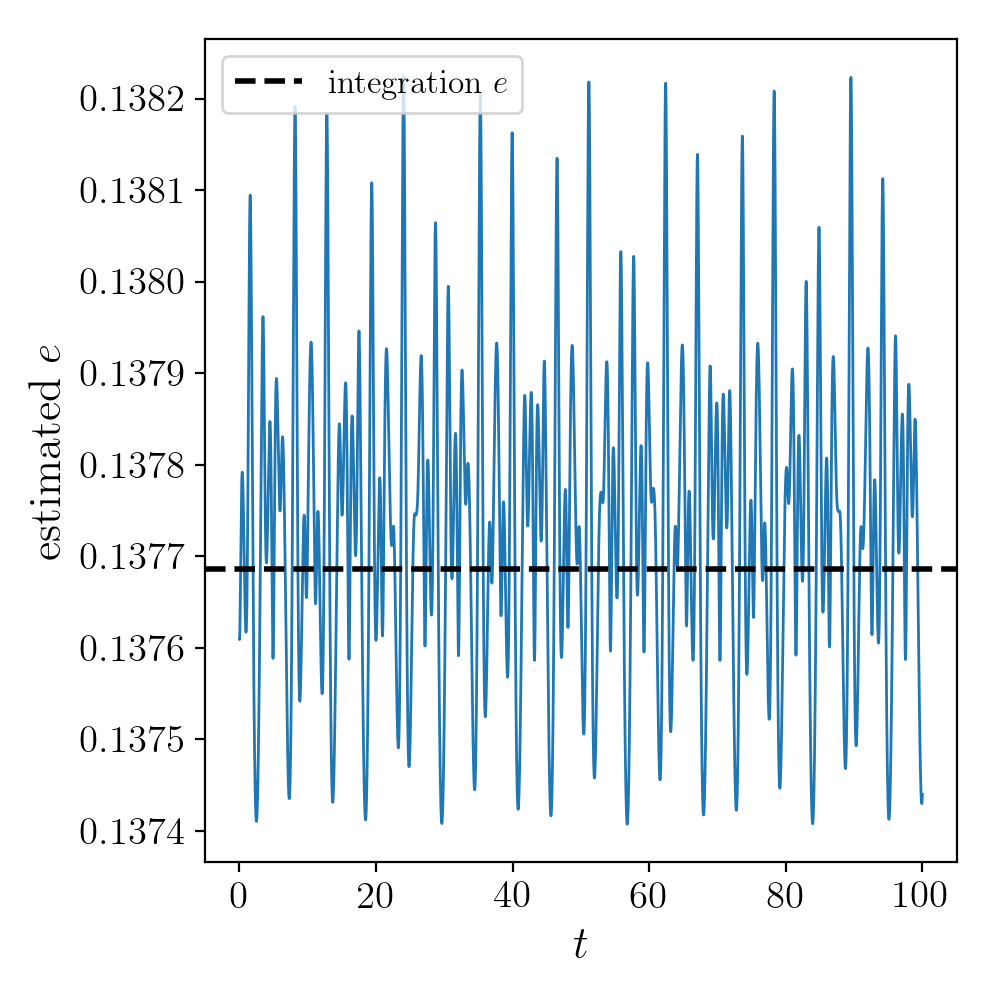
Accessing the raw orbit¶
The value of R, vR, vT, z, vz, x, vx,
y, vy, phi, and vphi at any time can be obtained by
calling the corresponding function with as argument the time (the same
holds for other coordinates ra, dec, pmra, pmdec,
vra, vdec, ll, bb, pmll, pmbb, vll,
vbb, vlos, dist, helioX, helioY, helioZ,
U, V, and W). If no time is given the initial condition is
returned, and if a time is requested at which the orbit was not saved
spline interpolation is used to return the value. Examples include
>>> o.R(1.)
# 1.1545076874679474
>>> o.phi(99.)
# 88.105603035901169
>>> o.ra(2.,obs=[8.,0.,0.],ro=8.)
# array([ 285.76403985])
>>> o.helioX(5.)
# array([ 1.24888927])
>>> o.pmll(10.,obs=[8.,0.,0.,0.,245.,0.],ro=8.,vo=230.)
# array([-6.45263888])
For the Orbit op that was initialized above with a distance scale
ro= and a velocity scale vo=, the first of these would be
>>> op.R(1.)
# 9.2360614837829225 #kpc
which we can also access in natural coordinates as
>>> op.R(1.,use_physical=False)
# 1.1545076854728653
We can also specify a different distance or velocity scale on the fly, e.g.,
>>> op.R(1.,ro=4.) #different velocity scale would be vo=
# 4.6180307418914612
For Orbit instances that contain multiple objects, the functions
above return arrays with the shape of the Orbit.
We can also initialize an Orbit instance using the phase-space
position of another Orbit instance evaluated at time t. For
example,
>>> newOrbit= o(10.)
will initialize a new Orbit instance with as initial condition the
phase-space position of orbit o at time=10.. If multiple times
are given, an Orbit instance with one object for each time will be
instantiated (this works even if the original Orbit instance
contained multiple objects already).
The whole orbit can also be obtained using the function getOrbit
>>> o.getOrbit()
which returns a matrix of phase-space points with dimensions [ntimes,nphasedim] or [shape,ntimes,nphasedim] for Orbit instances with multiple objects.
Fast orbit integration and available integrators¶
The standard orbit integration is done purely in python using standard
scipy integrators. When fast orbit integration is needed for batch
integration of a large number of orbits, a set of orbit integration
routines are written in C that can be accessed for most potentials, as
long as they have C implementations, which can be checked by using the
attribute hasC
>>> mp= MiyamotoNagaiPotential(a=0.5,b=0.0375,amp=1.,normalize=1.)
>>> mp.hasC
# True
Fast C integrators can be accessed through the method= keyword of
the orbit.integrate method. Currently available integrators are
rk4_c
rk6_c
dopr54_c
dop853_c
which are Runge-Kutta and Dormand-Prince methods. There are also a number of symplectic integrators available
leapfrog_c
symplec4_c
symplec6_c
The higher order symplectic integrators are described in Yoshida (1993). In pure Python, the available integrators are
leapfrog
odeint
dop853
For most applications I recommend symplec4_c or dop853_c,
which are speedy and reliable. For example, compare
>>> o= Orbit([1.,0.1,1.1,0.,0.1])
>>> timeit(o.integrate(ts,mp,method='leapfrog'))
# 1.34 s ± 41.8 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
>>> timeit(o.integrate(ts,mp,method='leapfrog_c'))
# galpyWarning: Using C implementation to integrate orbits
# 91 ms ± 2.42 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
>>> timeit(o.integrate(ts,mp,method='symplec4_c'))
# galpyWarning: Using C implementation to integrate orbits
# 9.67 ms ± 48.3 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
>>> timeit(o.integrate(ts,mp,method='dop853_c'))
# 4.65 ms ± 86.8 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
If the C extensions are unavailable for some reason, I recommend using
the odeint pure-Python integrator, as it is the fastest. Using the
same example as above
>>> o= Orbit([1.,0.1,1.1,0.,0.1])
>>> timeit(o.integrate(ts,mp,method='leapfrog'))
# 2.62 s ± 128 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
>>> timeit(o.integrate(ts,mp,method='odeint'))
# 153 ms ± 2.59 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
>>> timeit(o.integrate(ts,mp,method='dop853'))
# 1.61 s ± 218 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
NEW in v1.9 Surfaces of section¶
galpy can compute surfaces of section for two- and three-dimensional
orbits using a special integration method that exactly determines the
intersection between orbits and a surface of section. The implemented
method follows
Hunter et al. (1998)
in re-writing the integration in terms of an independent angular variable \(\psi\)
that is equal to a multiple of \(2\pi\) at intersections of the orbit with
a surface of section. For example, to compute the surface of section of a
three-dimensional orbit in an axisymmetric potential for the \(z=0,\,v_z>0\)
surface of section, we re-write the vertical phase-space coordinates as
When computing the surface of section of a two-dimensional orbit using either the
\(x=0,\,v_x>0\) or \(y=0,\,v_y>0\) surfaces, we proceed in a similar way.
As long as the surface of section is a symmetry plane of the potential, the angle
\(\psi\) increases monotonically with time and we can use \(\psi\) as the
independent variable in orbit integration rather than time. This allows us to
exactly integrate to integer multiples of \(\psi = 2\pi\) and compute the
surface of section. galpy only supports surfaces of section for the three cases
mentioned above, repeated here:
3D orbits: \(z=0,\,v_z>0\) surface;
2D orbits: \(x=0,\,v_x>0\) or \(y=0,\,v_y>0\) surfaces.
While galpy will happily compute the surface of section for any 3D or 2D orbit,
surfaces of section make most sense in 3D for static, axisymmetric potentials and
in 2D for static, non-axisymmetric potentials, like the examples below.
For some force fields, the reparameterization of the orbit in terms of
\(\psi\) does not work, because the angle \(\psi\) does not increase
monotonically with time. This is notably the case for many orbits integrated in
a non-inertial frame (e.g., bar orbits in the bar’s rotating frame). In these
cases, you can use a brute-force approach to determining the surface of section
implemented in Orbit.bruteSOS and Orbit.plotBruteSOS, which work
similarly to the Orbit.SOS and Orbit.plotSOS methods discussed below,
but simply look for surface crossings using a regular orbit integration. In this case,
you have to specify how long to integrate the orbit for and you can, therefore, not
directly control the number of crossings that you will get.
As an example, let’s consider the orbit of the Sun in MWPotential2014. To plot the
surface of section, simply do:
>>> from galpy.orbit import Orbit
>>> from galpy.potential import MWPotential2014
>>> o= Orbit()
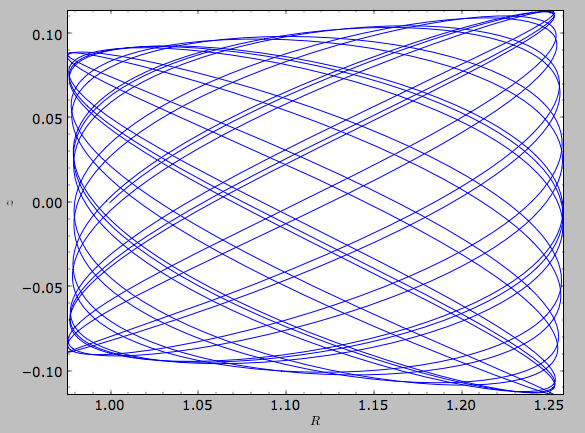
>>> o.plotSOS(MWPotential2014)
which gives
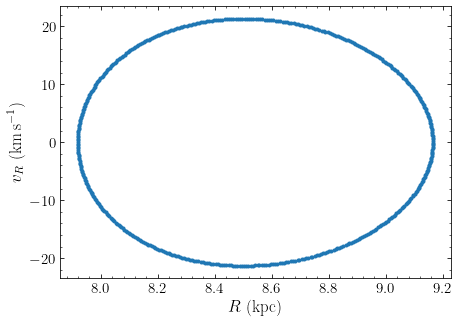
To get the values plotted here, do:
>>> Rs, vRs= o.SOS(MWPotential2014)
Warning
Computing the surface of section leaves the Orbit instance in a state where its
internally-stored integrated orbit is that computed during the surface-of-section
integration (any previously integrated orbit is overwritten). However, the orbit is
only output at intersections with the surface of section. Furthermore, with an
Orbit like that of the Sun above whose initial condition is not in the surface of
section, the first point along this orbit is not the initial condition, but the first
surface-of-section crossing instead. This is because for orbits like this, internally
galpy first integrates to the first crossing and then re-starts the integration
to obtain many subsequent crossings to create the surface of section.
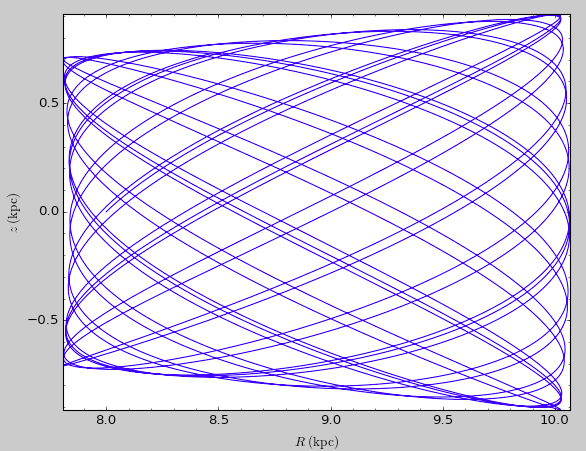
Surfaces of section can also be computed for Orbit instances that contain multiple orbits, e.g., for the following two orbits defined to have the same energy and angular momentum:
>>> from galpy.orbit import Orbit
>>> from galpy.potential import MWPotential2014, evaluatePotentials
>>> def orbit_RvRELz(R,vR,E,Lz,z_init=0.,pot=None):
"""Returns Orbit at (R,vR,phi=0,z=z_init) with given (E,Lz)"""
return Orbit([R,vR,Lz/R,z_init,
numpy.sqrt(2.*(E-evaluatePotentials(pot,R,z_init)
-(Lz/R)**2./2.-vR**2./2)),0.],ro=8.,vo=220.)
>>> R, E, Lz= 0.8, -1.25, 0.6
>>> twoorb= Orbit([orbit_RvRELz(R,0.,E,Lz,pot=MWPotential2014),
orbit_RvRELz(R,0.1,E,Lz,pot=MWPotential2014,z_init=0.1)])
>>> twoorb.plotSOS(MWPotential2014)
which gives
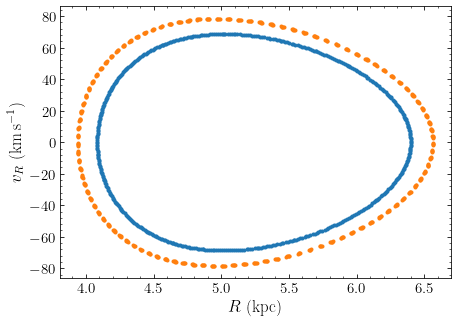
You can increase the number of points in the surface of section using the ncross=
keyword. For example, you will see the outer locus fill in with ncross=1500.
An example in two dimensions is given by the following box orbit in a non-axisymmetric cored logarithmic potential:
>>> from galpy.orbit import Orbit
>>> from galpy.potential import LogarithmicHaloPotential
>>> lp= LogarithmicHaloPotential(normalize=True,b=0.9,core=0.2)
>>> orb= Orbit([0.1,0.,lp.vcirc(0.1,phi=0.),numpy.pi/2.])
>>> orb.plotSOS(lp,surface='y') # default is surface='x'
which gives

Integration of the phase-space volume¶
galpy further supports the integration of the phase-space volume
through the method integrate_dxdv, although this is currently only
implemented for two-dimensional orbits (planarOrbit). As an
example, we can check Liouville’s theorem explicitly. We initialize
the orbit
>>> o= Orbit([1.,0.1,1.1,0.])
and then integrate small deviations in each of the four phase-space directions
>>> ts= numpy.linspace(0.,28.,1001) #~1 Gyr at the Solar circle
>>> o.integrate_dxdv([1.,0.,0.,0.],ts,mp,method='dopr54_c',rectIn=True,rectOut=True)
>>> dx= o.getOrbit_dxdv()[-1,:] # evolution of dxdv[0] along the orbit
>>> o.integrate_dxdv([0.,1.,0.,0.],ts,mp,method='dopr54_c',rectIn=True,rectOut=True)
>>> dy= o.getOrbit_dxdv()[-1,:]
>>> o.integrate_dxdv([0.,0.,1.,0.],ts,mp,method='dopr54_c',rectIn=True,rectOut=True)
>>> dvx= o.getOrbit_dxdv()[-1,:]
>>> o.integrate_dxdv([0.,0.,0.,1.],ts,mp,method='dopr54_c',rectIn=True,rectOut=True)
>>> dvy= o.getOrbit_dxdv()[-1,:]
We can then compute the determinant of the Jacobian of the mapping defined by the orbit integration from time zero to the final time
>>> tjac= numpy.linalg.det(numpy.array([dx,dy,dvx,dvy]))
This determinant should be equal to one
>>> print(tjac)
# 0.999999991189
>>> numpy.fabs(tjac-1.) < 10.**-8.
# True
The calls to integrate_dxdv above set the keywords rectIn= and
rectOut= to True, as the default input and output uses phase-space
volumes defined as (dR,dvR,dvT,dphi) in cylindrical coordinates. When
rectIn or rectOut is set, the in- or output is in rectangular
coordinates ([x,y,vx,vy] in two dimensions).
Implementing the phase-space integration for three-dimensional
FullOrbit instances is straightforward and is part of the longer
term development plan for galpy. Let the main developer know if
you would like this functionality, or better yet, implement it
yourself in a fork of the code and send a pull request!
Example: The eccentricity distribution of the Milky Way’s thick disk¶
A straightforward application of galpy’s orbit initialization and
integration capabilities is to derive the eccentricity distribution of
a set of thick disk stars. We start by downloading the sample of SDSS
SEGUE (2009AJ….137.4377Y) thick disk
stars compiled by Dierickx et al. (2010arXiv1009.1616D) from CDS at
this link.
Downloading the table and the ReadMe will allow you to read in the
data using astropy.io.ascii like so
>>> from astropy.io import ascii
>>> dierickx = ascii.read('table2.dat', readme='ReadMe')
>>> vxvv = numpy.dstack([dierickx['RAdeg'], dierickx['DEdeg'], dierickx['Dist']/1e3, dierickx['pmRA'], dierickx['pmDE'], dierickx['HRV']])[0]
After reading in the data (RA,Dec,distance,pmRA,pmDec,vlos; see above)
as a vector vxvv with dimensions [6,ndata] we (a) define the
potential in which we want to integrate the orbits, and (b) integrate
all orbits and compute their eccentricity numerically from the orbit
integration and analytically following the Staeckel
approximation method (the following takes lots of memory;
you might want to slice the orbits object to a smaller number to
run this code faster)
>>> ts= np.linspace(0.,20.,10000)
>>> lp= LogarithmicHaloPotential(normalize=1.)
>>> orbits= Orbit(vxvv,radec=True,ro=8.,vo=220.,solarmotion='hogg')
>>> e_ana= orbits.e(analytic=True,pot=lp,delta=1e-6)
>>> orbits.integrate(ts,lp)
>>> e_int= orbits.e()
We then find the following eccentricity distribution (from the numerical eccentricities)

The eccentricity calculated by integration in galpy compare well with those calculated by Dierickx et al., except for a few objects
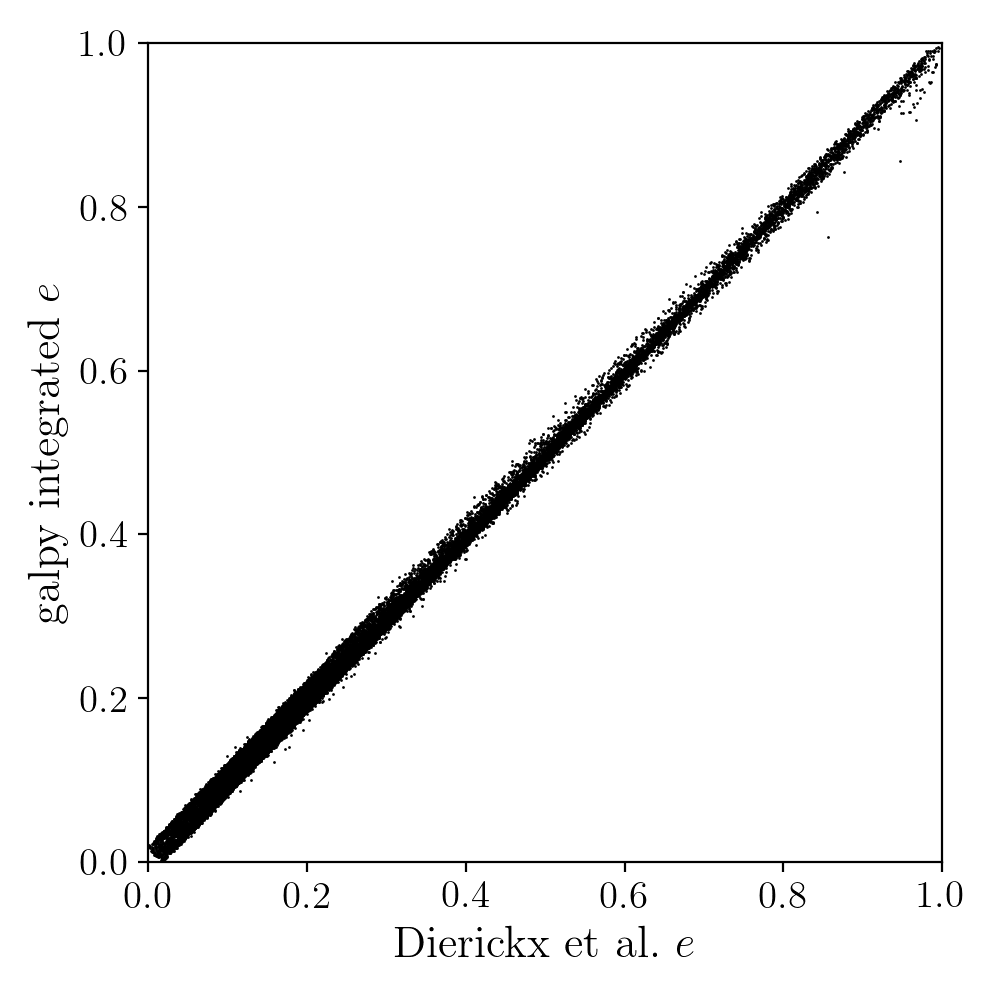
and the analytical estimates are equally as good:

In comparing the analytic and integrated eccentricity estimates - one can see that in this case the estimation is almost exact, due to the spherical symmetry of the chosen potential:
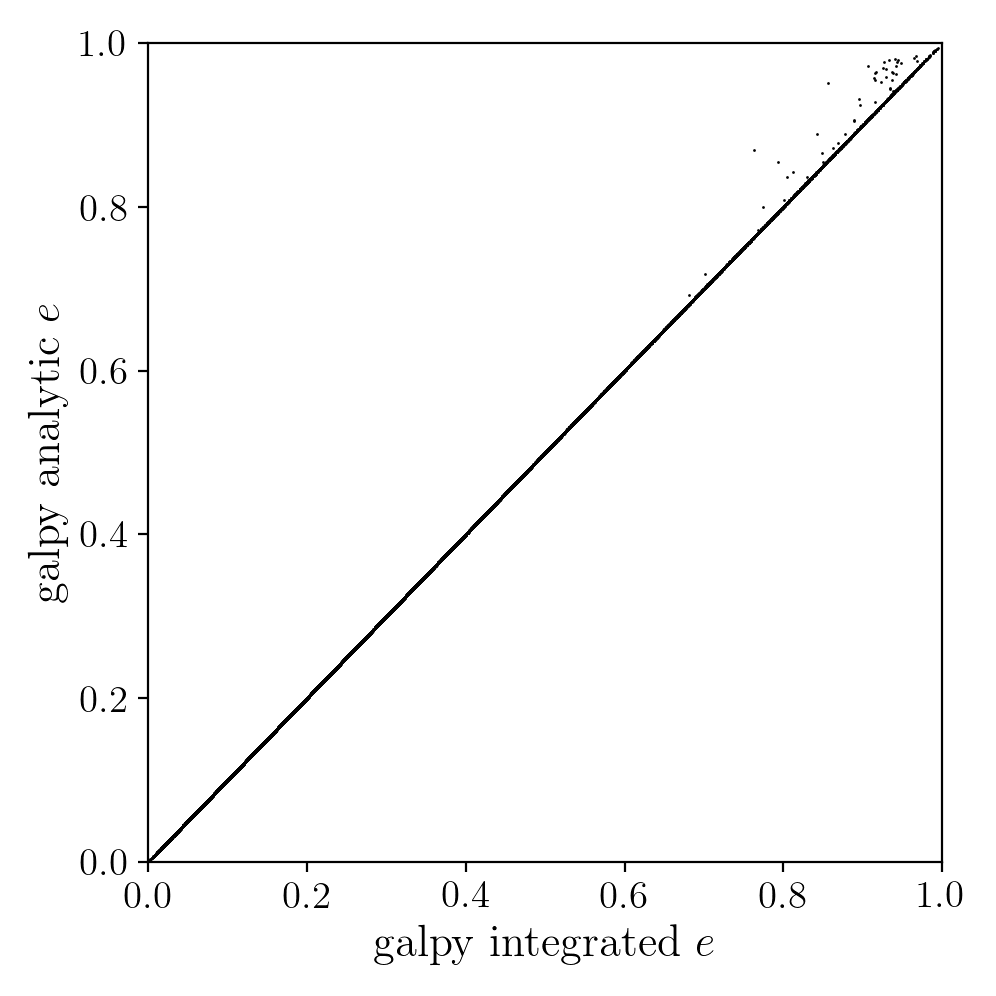
A script that calculates and plots everything can be downloaded
here. To generate the plots just run:
python dierickx_eccentricities.py ../path/to/folder
specifying the location you want to put the plots and data.
Alternatively - one can transform the observed coordinates into spherical coordinates and perform
the estimations in one batch using the actionAngle interface, which takes considerably less time:
>>> from galpy import actionAngle
>>> deltas = actionAngle.estimateDeltaStaeckel(lp, Rphiz[:,0], Rphiz[:,2], no_median=True)
>>> aAS = actionAngleStaeckel(pot=lp, delta=0.)
>>> par = aAS.EccZmaxRperiRap(Rphiz[:,0], vRvTvz[:,0], vRvTvz[:,1], Rphiz[:,2], vRvTvz[:,2], Rphiz[:,1], delta=deltas)
The above code calculates the parameters in roughly 100ms on a single core.
Example: The orbit of the Large Magellanic Cloud in the presence of dynamical friction¶
As a further example of what you can do with galpy, we investigate the Large Magellanic Cloud’s (LMC) past and future orbit. Because the LMC is a massive satellite of the Milky Way, its orbit is affected by dynamical friction, a frictional force of gravitational origin that occurs when a massive object travels through a sea of low-mass objects (halo stars and dark matter in this case). First we import all the necessary packages:
>>> from astropy import units
>>> from galpy.potential import MWPotential2014, ChandrasekharDynamicalFrictionForce
>>> from galpy.orbit import Orbit
(also do %pylab inline if running this in a jupyter notebook or
turn on the pylab option in ipython for plotting). We can load the
current phase-space coordinates for the LMC using the
Orbit.from_name function described above:
>>> o= Orbit.from_name('LMC')
We will use MWPotential2014 as our Milky-Way potential
model. Because the LMC is in fact unbound in MWPotential2014, we
increase the halo mass by 50% to make it bound (this corresponds to a
Milky-Way halo mass of \(\approx 1.2\,\times 10^{12}\,M_\odot\), a
not unreasonable value). We can adjust a galpy Potential’s amplitude simply by multiplying the potential by a number, so to increase the mass by 50% we do
>>> MWPotential2014[2]*= 1.5
Let us now integrate the orbit backwards in time for 10 Gyr and plot it:
>>> ts= numpy.linspace(0.,-10.,1001)*units.Gyr
>>> o.integrate(ts,MWPotential2014)
>>> o.plot(d1='t',d2='r')
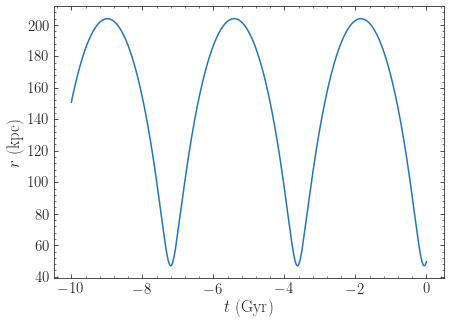
We see that the LMC is indeed bound, with an apocenter just over 200 kpc. Now let’s add dynamical friction for the LMC, assuming that its mass is \(5\times 10^{10}\,M_\odot\). We setup the dynamical-friction object:
>>> cdf= ChandrasekharDynamicalFrictionForce(GMs=5.*10.**10.*units.Msun,rhm=5.*units.kpc,
dens=MWPotential2014)
Dynamical friction depends on the velocity distribution of the halo, which is assumed to be an isotropic Gaussian distribution with a radially-dependent velocity dispersion. If the velocity dispersion is not given (like in the example above), it is computed from the spherical Jeans equation. We have set the half-mass radius to 5 kpc for definiteness. We now make a copy of the orbit instance above and integrate it in the potential that includes dynamical friction:
>>> odf= o()
>>> odf.integrate(ts,MWPotential2014+cdf)
Overlaying the orbits, we can see the difference in the evolution:
>>> o.plot(d1='t',d2='r',label=r'$\mathrm{No\ DF}$')
>>> odf.plot(d1='t',d2='r',overplot=True,label=r'$\mathrm{DF}, M=5\times10^{10}\,M_\odot$')
>>> ylim(0.,660.)
>>> legend(fontsize=17.)
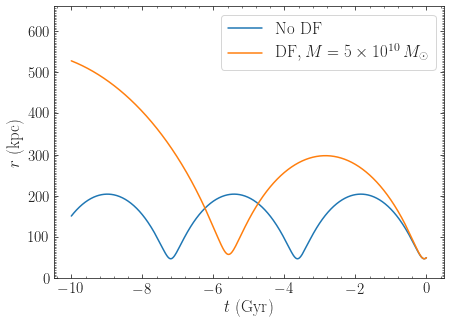
We see that dynamical friction removes energy from the LMC’s orbit, such that its past apocenter is now around 500 kpc rather than 200 kpc! The period of the orbit is therefore also much longer. Clearly, dynamical friction has a big impact on the orbit of the LMC.
Recent observations have suggested that the LMC may be even more massive than what we have assumed so far, with masses over \(10^{11}\,M_\odot\) seeming in good agreement with various observations. Let’s see how a mass of \(10^{11}\,M_\odot\) changes the past orbit of the LMC. We can change the mass of the LMC used in the dynamical-friction calculation as
>>> cdf.GMs= 10.**11.*units.Msun
This way of changing the mass is preferred over re-initializing the
ChandrasekharDynamicalFrictionForce object, because it avoids
having to solve the Jeans equation again to obtain the velocity
dispersion. Then we integrate the orbit and overplot it on the
previous results:
>>> odf2= o()
>>> odf2.integrate(ts,MWPotential2014+cdf)
and
>>> o.plot(d1='t',d2='r',label=r'$\mathrm{No\ DF}$')
>>> odf.plot(d1='t',d2='r',overplot=True,label=r'$\mathrm{DF}, M=5\times10^{10}\,M_\odot$')
>>> odf2.plot(d1='t',d2='r',overplot=True,label=r'$\mathrm{DF}, M=1\times10^{11}\,M_\odot$')
>>> ylim(0.,660.)
>>> legend(fontsize=17.)
which gives

Now the LMC barely performs a full orbit over the last 10 Gyr.
Finally, let’s see what will happen in the future if the LMC is as massive as \(10^{11}\,M_\odot\). We simply flip the sign of the integration times to get the future trajectory:
>>> odf2.integrate(-ts[-ts < 9*units.Gyr],MWPotential2014+cdf)
>>> odf2.plot(d1='t',d2='r')
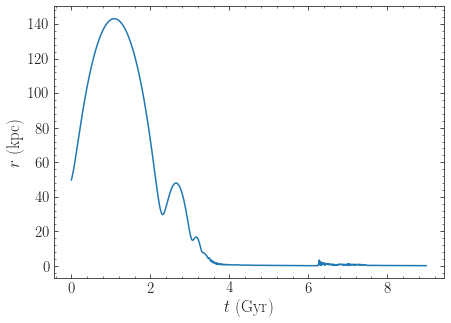
Because of the large effect of dynamical friction, the LMC will merge with the Milky-Way in about 4 Gyr after a few more pericenter passages. Note that we have not taken any mass-loss into account. Because mass-loss would lead to a smaller dynamical-friction force, this would somewhat increase the merging timescale, but dynamical friction will inevitably lead to the merger of the LMC with the Milky Way.
Warning
When using dynamical friction, if the radius gets very small, the integration sometimes becomes very erroneous, which can lead to a big, unphysical kick (even though we turn off friction at very small radii); this is the reason why we have limited the future integration to 9 Gyr in the example above. When using dynamical friction, inspect the full orbit to make sure to catch whether a merger has happened.
Example: Including the Milky Way center’s barycentric acceleration due to the Large Magellanic Cloud in orbit integrations¶
Observations over the last few decades have revealed that the Large Magellanic
Cloud (LMC) is so massive that it pulls the center of the Milky Way towards it to a
non-vanishing degree. This implies that the Galactocentric reference frame is
not an inertial reference frame and that orbit integrations should take the
fictitious forces due to the frame’s acceleration into account. In this example,
we demonstrate how this can be done in galpy in a simplified manner.
To take the Galactocentric frame’s acceleration into account, we use the
NonInertialFrameForce. This Force
class requires one to input the acceleration of the origin of the
non-inertial reference frame, so we first need to determine that. To do this
properly, one would have to run some sort of N-body simulation of the
LMC’s infall into the Milky Way. To avoid doing that, for the purpose of this
simple illustration, we will make the following approximation. We will first
compute the orbit of the LMC in the Milky Way, assuming that the Milky Way
remains at rest (and is thus an inertial frame), and then we will compute
the acceleration of the origin induced by the pull from the LMC along this
orbit. Because the effect of the LMC is rather small, this is a decent
approximation.
We therefore start by computing the orbit of the LMC in the past like in the
previous example in section Example: The orbit of the Large Magellanic Cloud in the presence of dynamical friction. We repeat the
code here for convenience (we choose again to increase the halo mass in
MWPotential2014 by 50% and we choose the heaviest LMC for this example)
>>> import numpy
>>> from astropy import units
>>> from galpy.potential import MWPotential2014, ChandrasekharDynamicalFrictionForce
>>> from galpy.orbit import Orbit
>>> o= Orbit.from_name('LMC')
>>> MWPotential2014[2]*= 1.5 # Don't run this if you've already run it before in the session
>>> cdf= ChandrasekharDynamicalFrictionForce(GMs=10.**11.*units.Msun,rhm=5.*units.kpc,
dens=MWPotential2014)
>>> ts= numpy.linspace(0.,-10.,1001)*units.Gyr
>>> o.integrate(ts,MWPotential2014+cdf)
We then define functions giving the acceleration of the origin due to the
gravitational pull from the LMC. To do this, we define a MovingObjectPotential
for the orbiting LMC and then evaluate its forces in rectangular coordinates. We’ll
model the LMC as a HernquistPotential, with mass and half-mass radius consistent
with what we used in the dynamical friction above):
>>> from galpy.potential import HernquistPotential, MovingObjectPotential
>>> lmcpot= HernquistPotential(amp=2*10.**11.*units.Msun,
a=5.*units.kpc/(1.+numpy.sqrt(2.))) #rhm = (1+sqrt(2)) a
>>> moving_lmcpot= MovingObjectPotential(o,pot=lmcpot)
and then we define the functions giving the acceleration of the origin. This is
slightly tricky, because there are currently no pre-defined functions giving the
force in rectangular coordinates and because evaluating forces at the origin is
numerically unstable due to galpy’s use of cylindrical coordinates internally.
So we will put the origin at a small offset to avoid the numerical issues at the
origin and define the rectangular forces ourselves. By placing the origin at
\(\phi=0\), the rectangular forces are simple:
>>> from galpy.potential import (evaluateRforces, evaluatephitorques,
evaluatezforces)
>>> loc_origin= 1e-4 # Small offset in R to avoid numerical issues
>>> ax= lambda t: evaluateRforces(moving_lmcpot,loc_origin,0.,phi=0.,t=t,
use_physical=False)
>>> ay= lambda t: evaluatephitorques(moving_lmcpot,loc_origin,0.,phi=0.,t=t,
use_physical=False)/loc_origin
>>> az= lambda t: evaluatezforces(moving_lmcpot,loc_origin,0.,phi=0.,t=t,
use_physical=False)
Directly using these accelerations in the NonInertialFrameForce is very
slow (because they have to be evaluated a lot during orbit integration),
so we build interpolated versions to speed things up:
>>> if o.time(use_physical=False)[0] > o.time(use_physical=False)[1]:
>>> t_intunits= o.time(use_physical=False)[::-1] # need to reverse the order for interp
>>> else:
>>> t_intunits= o.time(use_physical=False)
>>> ax4int= numpy.array([ax(t) for t in t_intunits])
>>> ax_int= lambda t: numpy.interp(t,t_intunits,ax4int)
>>> ay4int= numpy.array([ay(t) for t in t_intunits])
>>> ay_int= lambda t: numpy.interp(t,t_intunits,ay4int)
>>> az4int= numpy.array([az(t) for t in t_intunits])
>>> az_int= lambda t: numpy.interp(t,t_intunits,az4int)
Note that we use numpy.interp here as the interpolation function,
because if numba is installed, galpy
will automatically use it to try to build fast, C versions of the functions
of time in NonInertialFrameForce. For this, numba must be able to
compile the function and it can do this for numpy.interp (but not for
scipy interpolation functions).
With these functions defined, we can then set up the NonInertialFrameForce
with this acceleration of the origin
>>> from galpy.potential import NonInertialFrameForce
>>> nip= NonInertialFrameForce(a0=[ax_int,ay_int,az_int])
As an example, let’s compute the past orbit of the Sun with and without taking the acceration of the origin into account. We’ll look at how the x position changes in time. When taking the acceleration of the origin into account, it is important to also include the acceleration due to LMC itself. Without it, the potential is inconsistent, e.g., the origin itself would move in the frame in which it is supposed to be at rest!
>>> sunts= numpy.linspace(0.,-3.,301)*units.Gyr
>>> osun_inertial= Orbit()
>>> osun_inertial.integrate(sunts,MWPotential2014)
>>> osun_inertial.plotx(label=r'$\mathrm{Inertial}$')
>>> osun_noninertial= Orbit()
>>> osun_noninertial.integrate(sunts,MWPotential2014+nip+moving_lmcpot)
>>> osun_noninertial.plotx(overplot=True,label=r'$\mathrm{Non-inertial}$')
>>> plt.legend(fontsize=18.,loc='upper left',framealpha=0.8)
This gives
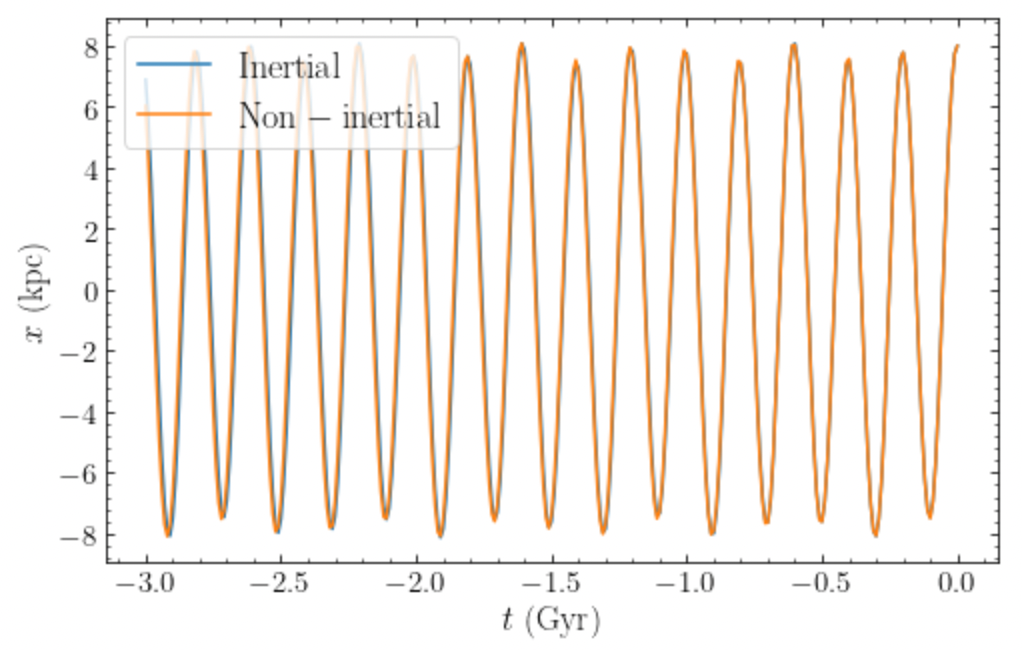
We see that there is essentially no difference. This is because the acceleration of the origin due to the LMC is much smaller than the acceleration felt by the Sun during its orbit from the Milky Way and the Sun is so close to the Galactic center relative to the LMC that much of the acceleration of the origin is cancelled by the attraction to the LMC (which at the center are equal in magnitude and opposite in sign). However, if we look at a dwarf galaxy orbiting far in the halo, we do notice small differences. For example, let’s look at the orbit of Fornax over the past 10 Gyr
>>> fornaxts= numpy.linspace(0.,-10.,101)*units.Gyr
>>> ofornax_inertial= Orbit.from_name('Fornax')
>>> ofornax_inertial.integrate(fornaxts,MWPotential2014)
>>> ofornax_inertial.plotr(label=r'$\mathrm{Inertial}$')
>>> ofornax_noninertial= Orbit.from_name('Fornax')
>>> ofornax_noninertial.integrate(fornaxts,MWPotential2014+nip+moving_lmcpot)
>>> ofornax_noninertial.plotr(overplot=True,label=r'$\mathrm{Non-inertial}$')
>>> plt.autoscale()
>>> plt.legend(fontsize=18.,loc='lower right',framealpha=0.8)
This gives
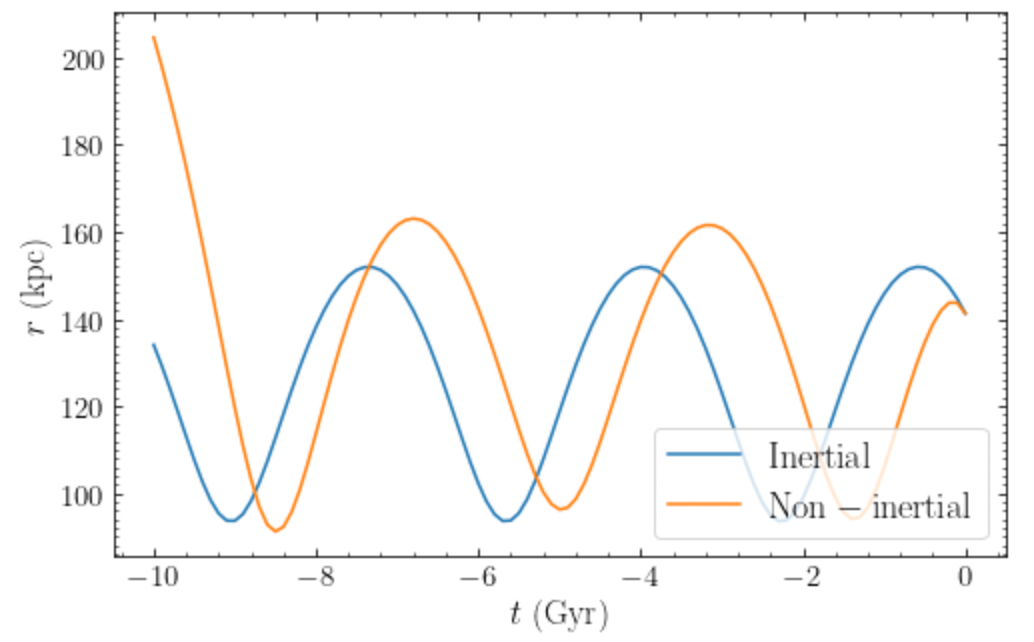
Now we see that there are significant differences in the past orbit when we take the acceleration of the Galactocentric reference frame into account. The reason that the orbit changes abruptly at \(-8\,\mathrm{Gyr}\) is because the LMC has a previous pericenter passage then in the orbit that we calculated for it, leading to a significant fictitious acceleration force at that time. Whether this is correct is of course highly uncertain.
To check whether the acceleration of the Milky Way’s origin that we obtained using the simple approximation above is realistic, we can, for example, compare to the results shown in Figure 10 of Vasiliev et al. (2021). This figure displays the displacement of the Milky Way’s origin and its velocity as a function of time, and also the fictitious force induced by the acceleration of the origin (this is minus the acceleration). To compute these quantities for the model above, we simply integrate the acceleration (starting 3 Gyr ago like Vasiliev et al.):
>>> from scipy import integrate
>>> from galpy.util import conversion
>>> vo, ro= 220., 8.
>>> int_ts_phys= numpy.linspace(-3.,0.,101)
>>> int_ts= int_ts_phys/conversion.time_in_Gyr(vo,ro)
>>> ax4plot= ax_int(int_ts)
>>> ay4plot= ay_int(int_ts)
>>> az4plot= az_int(int_ts)
>>> vx4plot= integrate.cumulative_trapezoid(ax4plot,x=int_ts,initial=0.)
>>> vy4plot= integrate.cumulative_trapezoid(ay4plot,x=int_ts,initial=0.)
>>> vz4plot= integrate.cumulative_trapezoid(az4plot,x=int_ts,initial=0.)
>>> xx4plot= integrate.cumulative_trapezoid(vx4plot,x=int_ts,initial=0.)
>>> xy4plot= integrate.cumulative_trapezoid(vy4plot,x=int_ts,initial=0.)
>>> xz4plot= integrate.cumulative_trapezoid(vz4plot,x=int_ts,initial=0.)
>>> plt.figure(figsize=(11,3.5))
>>> plt.subplot(1,3,1)
>>> plt.plot(int_ts_phys,xx4plot*ro,color=(0.5,0.5,247./256.),lw=2.,
label=r'$x$')
>>> plt.plot(int_ts_phys,xy4plot*ro,color=(111./256,180./256,109./256),lw=2.,
label=r'$y$')
>>> plt.plot(int_ts_phys,xz4plot*ro,color=(239./256,135./256,132./256),lw=2.,
label=r'$z$')
>>> plt.xlabel(r'$\mathrm{time}\,(\mathrm{Gyr})$')
>>> plt.ylabel(r'$\mathrm{displacement}\,(\mathrm{kpc})$')
>>> plt.legend(frameon=False,fontsize=18.)
>>> plt.subplot(1,3,2)
>>> plt.plot(int_ts_phys,vx4plot*vo,color=(0.5,0.5,247./256.),lw=2.)
>>> plt.plot(int_ts_phys,vy4plot*vo,color=(111./256,180./256,109./256),lw=2.)
>>> plt.plot(int_ts_phys,vz4plot*vo,color=(239./256,135./256,132./256),lw=2.)
>>> plt.xlabel(r'$\mathrm{time}\,(\mathrm{Gyr})$')
>>> plt.ylabel(r'$\mathrm{velocity}\,(\mathrm{km\,s}^{-1})$')
>>> plt.subplot(1,3,3)
>>> plt.plot(int_ts_phys,-ax4plot*conversion.force_in_kmsMyr(vo,ro)*1000.,
color=(0.5,0.5,247./256.),lw=2.)
>>> plt.plot(int_ts_phys,-ay4plot*conversion.force_in_kmsMyr(vo,ro)*1000.,
color=(111./256,180./256,109./256),lw=2.)
>>> plt.plot(int_ts_phys,-az4plot*conversion.force_in_kmsMyr(vo,ro)*1000.,
color=(239./256,135./256,132./256),lw=2.)
>>> plt.xlabel(r'$\mathrm{time}\,(\mathrm{Gyr})$')
>>> plt.ylabel(r'$\mathrm{acceleration}\,(\mathrm{km\,s}^{-1}\,\mathrm{Gyr}^{-1})$')
>>> plt.tight_layout()
and we obtain
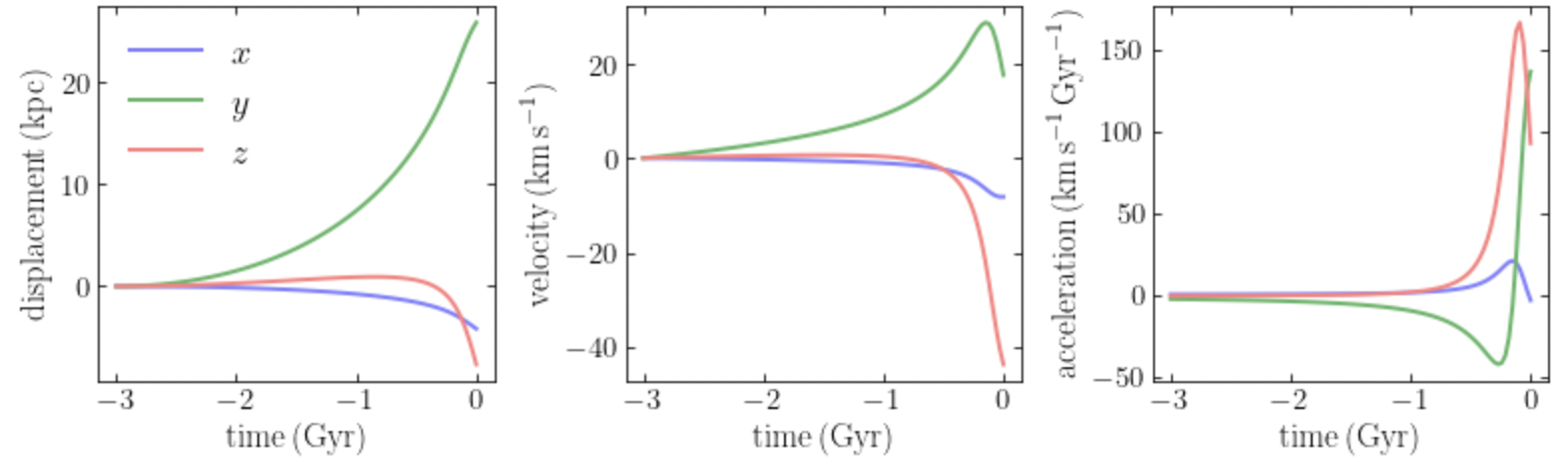
The main trends and magnitudes in this figure are the same as those in figure 10 of Vasiliev et al., so the acceleration of the origin that we computed here is reasonable. Note that Vasiliev et al. use a different LMC mass and that other aspects of their modeling differ (like the Milky Way’s potential), so we don’t expect an exact match.
